問題25　（リンデン　さん）　　

△ＡＢＣは∠Ａ＝１３５°、∠Ｂ＝１５°ＡＢ＝２ｃｍを満たすとします。
（１）　△ＡＢＣの面積を求めてください。
（２）　辺ＢＣ上の点Ｐを∠ＢＡＰ＝６０°をみたすようにとるとき、ＢＰ：ＰＣを求めてください。
　　　BP:PC=○:1　とし　○に当てはまる数を求めてください。

答えは小数で表すことにします。小数第４位を四捨五入し、小数第３位まで求めてください。
答えが4.6なら　4.6でも　4.600でもどちらでも正解とします。√があれば　それは　小数にしてください。

解答　（１）　0.732　　　(2)　1.732

(1)

図のように一辺の長さが2cmの正方形CDBEと　一辺の長さが　２の正三角形ABEを組み合わせると
三角形ABCがこの図形の中に埋め込まれていることがわかります。
この三角形ABCの面積は　正三角形ABE+三角形ACE-直角二等辺三角形BCEですから
1/2×2×√3+1/2×2×1-1/2×2×2=√3-1=0.732です

(2)
さらに　条件を満たす点PはAEとBCの交点になっていますから　EAの延長とCDの交点をQとすると
三角形CPQと三角形BPEが相似ですから
　BP:CP=BE:CP=CE:CQ　
三角形ECQは90度　60度　30度の直角三角形ですからBP:CP=√３:1=1.732：1となります。

解答2（ナキイルカさんの解答をもとに）


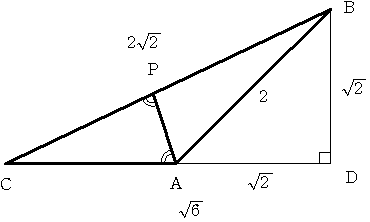
三角形ABCは　直角二等辺三角形ABD　と　30度　60度　90度の直角三角形BCDを
重ね合わせたものであるから　AD=√２　BD=√２
　　　　　　　　　　　　　　　　　　　CD=√６　　BC=2√２
(1)　三角形ABCの面積=1/2×AC×BD=1/2×(√6-√２)×√２=√3-1
(2)　三角形ACPは角CAP=角CPA=75度の二等辺三角形であるから
　　　CP=AP=√6-√２　　BP=BC-CP=2√２-(√6-√２)=３√２-√6=√3(√６-√2)　より
　　　CP:BP=1:√3

解答3（信三さん　みずきさん　の解答）

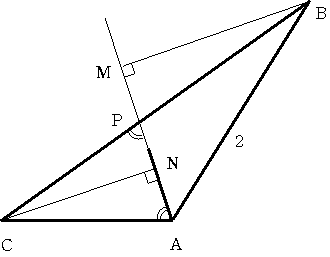
APを延長してそれへのBからの垂線の足をMとし、CからAPへの垂線の足をNとする。
三角形BAMは正三角形の半分で、BA＝２だから
MB＝３の平方根　「以下で　r３　と書く」
AM＝１
BCは角ABMの２等分線だから、MP：AP＝r３：２
NはAPの中点だから　MP：NP＝r３：１
r３：１　が　三角形BMPとCNPの相似の比となる。
従って　BP：PC＝r３：１
また　CN＝１
三角形ABCの面積は　AP＊（BM＋CN）／２
AP=1×2/(r3+2)=2/(r3+2)
より　2/(r3+2)×(r3+1)/2
これを計算して　r３−１　となる。