���23�@�itomh�@����j�@�@

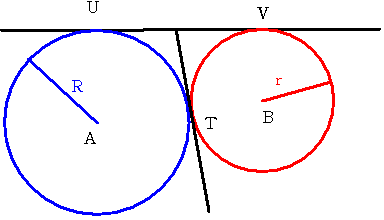
��F�~A�Ɖ~B���_T�ŊO�ڂ��Ă��܂�(�}���Q��)�B
�~A�̔��a��R�A�~B�̔��a��r�Ƃ��܂��iR>r�j�B
2�~�̋��ʐڐ��̂����iT��ʂ�Ȃ��j1�{���Ƃ�A
�~A�Ƃ̐ړ_��U�A�~B�Ƃ̐ړ_��V�ƌĂт܂��傤�B
���̂Ƃ��A��UT�ƌ�VT�ł́A�ǂ��炪�����ł��傤���H
��(tomh����j
�~A�̓_T��ʂ钼�a�́A�_T�̔��Α��̓_��S�Ƃ��܂��B
�_S,T����A���ꂼ�꒼��ST�̐����������A����UV�Ƃ̌�_���A���ꂼ��
M,N�Ƃ��܂��B���̂Ƃ��A
�@UN = TN = VN,
�@SM = UM,
�@TN < SM
�����藧���܂��B����āAVN<UM�ł��B
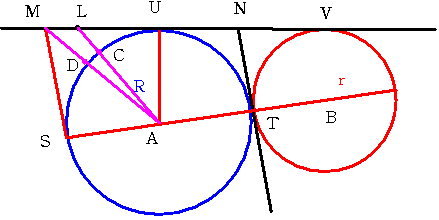
����ƁA����UM��������āAUL=VN�ł���悤�ȓ_L���Ƃ邱�Ƃ��ł��܂��B
�����āA����AL�Ɖ~A�Ƃ̌�_��C�A����AM�Ɖ~A�Ƃ̌�_��D�Ƃ��܂��B
����MC���~A�̊O���ɂ��邱�Ƃɒ��ӂ���ƁA
�@UM/UL = 1 +LM/UL
�@�@�@�@= 1 +��ALM/��ALU
�@�@�@�@= 1 +��ACM/��ACU
�@�@�@�@> 1 +��`ACD/��`ACU
�ƂȂ�܂��B�i"���c"��"��`�c"�́A���ꂼ��̐}�`�̖ʐς�\���܂��B�j
�X�ɕό`�𑱂���ƁA
�@UM/UL > 1 +��`ACD/��`ACU
�@�@�@ �@ = 1 +��CD/��CU = ��UD/��UC
�@�@�@�@�@= (��US/2)/(��UT/2) = ��US/��UT�@�c(1)�@�@�@�@�@�ł��B
���Ɏl�p�`MSAU��NTBV�͑����Ȃ̂ŁA
�@��US/��VT = UM/VN = UM/UL�@�c(2)�@�@�@�ƂȂ�܂��B
(1)��(2)���ׂ�ƁA
�@��US/��VT > ��US/��UT
�@��UT > ��VT�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�ƂȂ�܂��B
�@�� �i�~�̔��a�Ɋւ�炸�j��UT�̕�����VT��蒷���B
�Q�itomh����j
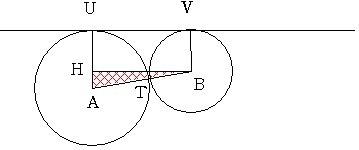
�~B�̒��S���璼��AU�����������A���̑���H�Ƃ��܂��B
�܂��A�pHBA=�ӂƂ����܂��B
�ӂ̓�����͈͂�
���̂Ƃ��A
�@��UT = R(��/2-��),
�@��VT = r(��/2+��)
�ƂȂ�̂ŁA�����Ƃ��āA
�@��(R-r)/2 -��(R+r)
�̐����ׂ邱�ƂɂȂ�܂��B
�����ŁA���ӂ��Ȃ���Ȃ�Ȃ��̂́A�p�����[�^�ӂ�R��r�ɂ����
���܂��Ă��܂��ʂȂ̂ŁA�Ɨ��ϐ��ł͂Ȃ����Ƃł��B�ł�����A
���̎���P���ɃӂŔ��������Ⴂ���Ȃ���ł��˂��B
�ŁA�ǂ����邩�Ƃ����ƁA
�@sin�� = AH/AB = (R-r)/(R+r)
�Ƃ��������g���āA
�@��(R-r)/2 -��(R+r) = [(R+r)/2] (��sin��-2��)�@�c�@(A)
�ƕό`���āA�i2(R+r)�͕K�����Ȃ̂Łj��sin��-2�ӂ̐����ׂ邱�Ƃ�
���܂��B����Ȃ�A�ӂŔ������Ă����v�ł��B
���ہA�����ׂĂ݂�ƁA�i0<��<��/2�͈̔͂Łj��sin��-2��>0��
������܂��B����āA�u��UT�̕�����VT��蒷���v���ƂɂȂ�܂��B
�Ƃ���ŁA����"��sin��-2��>0"�Ƃ����s�����́A"Jordan�̕s����"��
�Ă�Ă���L���ȕs�����Ȃ����ł��B�ؖ����@���F�X���邻��
�Ȃ̂ŁA�����������ꂽ���͌������Ă݂ĉ������B
���ӓ_�́A�u�������C�y�ɂ�����ʖ�!�v�Ƃ������Ƃł��B
�⑫�i�ق��j
�O���t����@����OQ�̌X���@�Ɓ@����OP�̌X�����l���ā@sin��/��>�P/(��/2)�@����
sin��/��>2/�@
��sin��>2��
��sin��-2��>0�@�ƂȂ�܂�
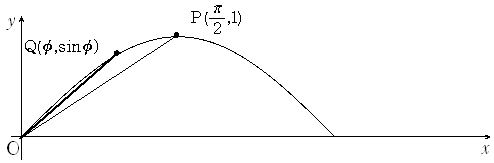
���iUnderBird����j�@�@
T��ʂ鋤�ʐڐ��Ɛ���UV�̌�_��W�Ƃ���B
���̂Ƃ��AUW=WV=WT�Ŏl�p�`AUWT�Ǝl�p�`WVBT�͑����ł��邱�Ƃ��e�Ղɂ킩�邩��A
UW=���Ƃ����Ɓ@�@�@�@�@�@�@�@�@�@AU:WV=UW:VB���@
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@R:x=x:r���Ƃ��āA
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@x=��(Rr)
��UAT=��(rad)�@[��ӂ��0<��<��/2�Ƃ��Ă悢]�Ƃ����ƁA
��UWT=�|�ƂŁ@�O�p�`UAT�ƎO�p�`UWT�ɗ]���藝��p�����
�@�@�@R^2�{R^2�|2�ER�ER�Ecos��={��(rR)}^2+{��(rR)}^2-2�E��(rR)�E��(rR)�Ecos(��-��)�@����
�@�@�@R=r(1+cos��)/(1-cos��)
�܂��A��UT=R�ƁA��VT=r(�|��)�@������A
�@�@�@R�Ɓ|r(�|��)
�@�@=r��(1+cos��)/(1-cos��)�|r(�|��)�@�@�@�@
�@�@ =r{2��/(1-cos��)�|��}
f(��)=2��/(1-cos��)�|�Ƃ���
�@�@f ' (��)=2(1-cos��-��sin��)/(1-cos��)^2�@�@�@
�����ŁA0<��<��/2�ŏ��(1-cos��)^2>0������@
�@�@�@�@�@g(��)=1-cos��-��sin�ƂƂ����Ɓ@
�@�@�@�@�@�@�@�@g ' (��)=-��cos��<0(0<��<��/2)�@�@�@�@�@�@�@�@�@�@�@�@
�@�@�@�@�@�@�@�@g(��)��0<��<��/2�Ō����ł���@��(0)=0�ł��邩��@
�@�@�@�@�@�@�@�@0<��<��/2�ɂ����ā@g(��)<0�@�ƂȂ�@�@f ' (��)<0�ł��邱�ƂɂȂ�@�@
����āAf(��)��0<��<��/2�Ō����ł���A
f(��/2)=0������A
0<��<��/2�ł́AR�Ɓ�r(�|��)����āA��UT����VT
���inobu����j�@�@
���ʐڐ��̌�_��O�Ƃ��܂��B
�ڂt�n�s�{�ڂu�n�s���@�@�@�ڂt�n�s���ڂu�n�s�ł��邱�Ƃ��
�ڂt�n�s���^�Q�{���A�ڂu�n�s���^�Q�|���@�i�O�������^�Q�j�Ƃ����܂��B
�܂��A�ڂ`�t�n���ڂ`�s�n���ڂa�s�n����BVO���X�O���ł��邱�Ƃ���
�ڂt�`�s���ڂu�n�s�A�ڂu�a�s���ڂt�n�s�@
�������ڂt�`�s���i�q�|���j�^�i�q�{���j�������i�^�Q�|���j���i�q�|���j�^�i�q�{���j
�q�|�����i�q�{���j�~�������i�^�Q�|���j
�@��UT�|��VT ���q�~�i�^�Q�|���j�|���~�i�^�Q�{���j
���i�q�|���j�~ �^�Q �| �i�q�{���j�~��
���i�q�{���j�~�������i�^�Q�|���j�~�^�Q �| �i�q�{���j�~��
�� �i�q�{���j�~�i���������~�^�Q �| ���j
�����ł��i���j�� ���������~�^�Q �| �� �i�O�������^�Q�j �Ƃ���
���f�i���j�� ���������~�^�Q �| �P
���f�f�i���j���| ���������~�^�Q ���O
���f�i���j�͒P�������A���f�i�O�j�� �^�Q �| �P���O�C ���f�i�^�Q�j��
�| �P���O
������@���f�i���j���O�@�ƂȂ�@���i�O�������^�Q�j�@�����݂��A
���i���j�� �O�������� �ő����A ���������^�Q �Ō����B
���i�O�j���O�C ���i�^�Q�j��1�~�^�Q �|�^�Q��0�@�@�@�@
�ȏ���A�O�������^�Q�@�͈̔͂Ł@���i���j���O�@���������B
�䂦�Ɂ@��UT�|��VT ���O���Ȃ킿�@��UT�̕�����VT��蒷���B
���ikasama����j�@
���}�̂悤�ɓ_B�������AU�ɐ������Ђ�����AB�Ƃ̂Ȃ��p���ƂƂ��܂��B
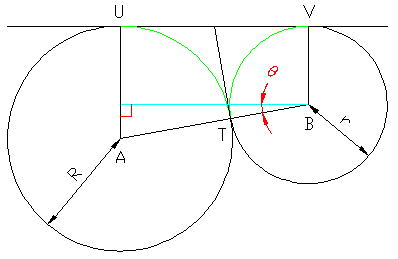
����ƁA
�@��TU=R(��/2-��)�A��TV=r(��/2+��)
�ł�����A��TU�ƌ�TV�̍��ׂ�ǂ��炪�������킩��܂���(*^_^*)�B
�@��TU-��TV=R(��/2-��)-r(��/2+��)=��(R-r)/2-(R+r)��=��(R-r)/2-(R+r)sin-1{(R
-r)/(R+r)}���(��)
�ł��B�����ŁAsin(��)=(R-r)/(R+r)�˃�=sin-1{(R
-r)/(R+r)}�ł��B
���`�ƁA����ŁA�T�C���J�[�u�̉��������߂钼�����C���[�W���܂��āA
�@0<x<��/2�Ȃ�2x/��<sin(x)��x<sin(��x/2)�˃�x/2<sin-1(x)�@�@...�@
�ł��B�����(��)�ɓK�p���܂��ƁA
�@��TU-��TV>��(R-r)/2-(R+r)��(R-r)/(R+r)/2=0
�܂�A��TU����TV��蒷����ł��B
���i��낳��j�@
�����t�u�ƒ����`�a�̌�_�̍��p���ƂƂ����
�O���Ɓ��X�O��
���̎�
�O��sin�Ɓ��P
�q/sin�Ɓ@�|�@��/sin�Ɓ@���@�q�{r
r�@���@�q�i�P�|sin�Ɓj/�i�P�{sin�Ɓj
�ǂt�s�ƌǂu�s�Ƃ̍������ɂ����
�Q�q�i�X�O�|�Ɓj/�R�U�O�|�Q�q�i�X�O�{�Ɓj/�R�U�O*�i�P�|sin�Ɓj/�i�P�{sin�Ɓj
���Q�q��/�R�U�O�o�i�X�O�|�Ɓj�|�i�P�|sin�Ɓj/�i�P�{sin�Ɓj�@�~�@�i�X�O�{�Ɓj�p
���Q�q��/�R�U�O�i�P�{sin�Ɓj�@�~�@�o�i�X�O�|�Ɓj�i�P�{sin�Ɓj�|�i�P�|sin�Ɓj�i�X�O�{�Ɓj�p
���S�q��/�R�U�O�i�P�{sin�Ɓj�@�~�@�i�X�O*sin�Ɓ|�Ɓj
���̎�
�S�q��/�R�U�O�i�P�{sin�Ɓj�͏�ɐ��ƂȂ�B
�X�O*sin�Ɓ|�Ɓ��X�O�isin�Ɓ|��/�X�O�j
�x��sin�Ƃ̃O���t�͂O���Ɓ��X�O�͈̔͂�
�x����/�X�O�̃O���t�̏�ɂ���̂�
sin�Ɓ|��/�X�O����ɐ��ɂȂ�B
����Čǂt�s�|�ǂu�s���O
�ƂȂ�̂ŁA�ǂt�s�̕��������B
���iuchinyan����j
�ȉ��ł́A�p�x�͌ʓx�@���g���܂��B
��UAT = �� �Ƃ��܂��B
T �͋��ʓ��ڐ��̐ړ_�Ȃ̂ŁAA�A T�A B �͈꒼����ɂ���܂��B
�����ŁA��UABV ���l����ƁA��VUA = ��UVB = ��/2 �Ȃ̂ŁA��VBT = ��-�� �ƂȂ�A
��UT = R�ƁA�@��VT = r(��-��)�A�@cos�� = (R-r)/(R+r)�@�@�ł��邱�Ƃ��킩��܂��B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�i�Ȃ��AR > r ���A0
< �� < ��/2 �ł��B�j
���At = R/r > 1 �Ƃ����āA���̎��@F�@���l���܂��B
F = ��UT - ��VT = R�� - r(��-��) = (R+r)�� - r�� = r{(t+1)��-��}
�܂��@�@cos�� = (t-1)/(t+1) = 1 - 2/(t+1)�ƂȂ��Ă��܂�
F �̐������ʂ̒����̑召�����肵�܂��B
�����Ł@�����Ƃ��ā@�� = ��/(t+1) �Ƃ����@cos����cos�� ���r���܂��B
x = 1/(t+1) �Ƃ����ƁA�@0 < x < 1/2 �ŁAcos�� = cos(��x) �� cos��
= 1 - 2x �Ƃ�
��r����悢���ƂɂȂ�܂��B
0 < x < 1/2 �ł́Acos �́A���ŁA�P���������ɂȂ��Ă��܂��B
���āA���̓�� cos�̑召 �́A��̊�y = cos(��x)�@�@����с@y = 1
- 2x��
�O���t�������Ă݂�Ƃ킩��܂����Acos �́A0 < x < 1/2�ŏ�ɓʂȂ̂ŁA
cos�� = cos(��x) > 1 - 2x = cos�Ƃƕ�����܂��B
����ā@cos �̒P�����������A�� < �ƂƂȂ�܂��B
������g����
F = r{(t+1)��-��}>r{(t+1)��-��}=0
���������āA��UT > ��VT �ł��邱�Ƃ�������܂��B