�@50�~10��3 = 500/3�p3
�ł��B�Ȃ̂ŁA�W�̎O�p���̑̐ς�
�@125/6�p3 �~ 8�@���(1)
�ł��B
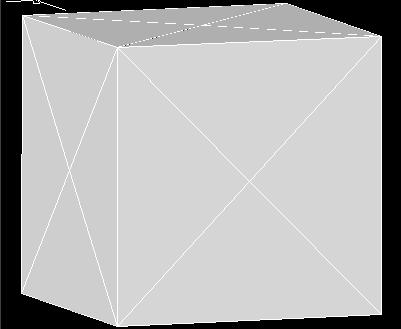
�C�㉺�ɕ���
�A�̒����ɂ��闧�̂��㉺�Ɉ����L���悤�ɂ��ĕ������܂��B

����ƁA�}�̒����t�߂ɂW�̎l�p��������܂���^^�B
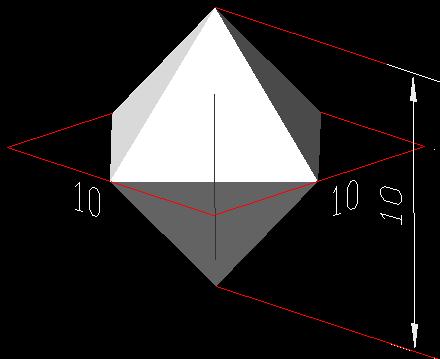
�D�W�̎l�p���̑̐�
�W�̎l�p���̂����܂���ォ�猩��ƁA
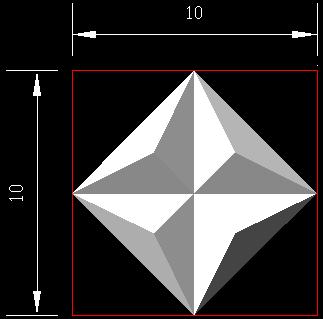
��ӂ�10�p�̐����`�̒��Ɏ��܂��Ă��邱�Ƃ��킩��܂��B�܂��A�����猩��ƁA

������10/3�p�ł��邱�Ƃ��킩��܂���^^�B�Ȃ̂ŁA���̗��̂̑̐ς�
�@50�~10/3��3 = 500/9�p3
�ł���A�W�̎l�p���̑̐ς�
�@125/18�p3 �~ 8�@���(2)
�ł��B
�E�㉺�̗���
�C�̕����łł����㉺�̗��̂��W�ɕ������܂��傤�B

�}�`�̑Ώ̐����炱�̂����̂P�ׂ�Ηǂ��Ǝv���܂��B�Ȃ��A���̂P�̗��̂̑̐ς́A(1)�A(2)������A
�@{1000 - (500/3 + 500/9)}��8 = 875/9�p3�@��� (3)
�ł��邱�Ƃ��킩��܂��B���āA���̐}�`�ɂ͂Q�̎O�p�����͂ݏo���Ă���̂��킩��܂����B�����𑵂��邽�߂ɉ��}�̂悤�Ɉړ������܂��傤�B

���̂悤�ɂ���ƁA�������ꂽ���̐}�`�̍��͂��ׂē����ł��邱�Ƃ��킩��܂��B����ɁA��̐}�`���Ђ�����Ԃ��ƁA
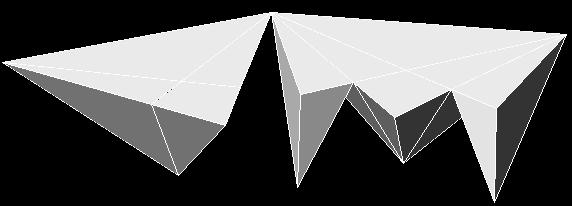
�̂悤�ɂȂ�A�Ȃ���ƁA
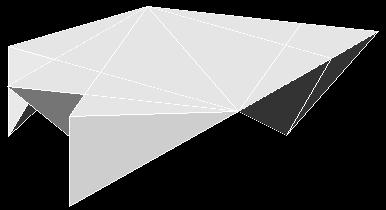
�ƂȂ�܂��B��ɂ��q�ׂ��悤�ɁA�����̐}�`�͍������������̂ŁA��ʂ������l�@���܂��B�����Ȑ}�`��F��������ƁA

�ƂȂ�܂��B�ӂ̔���
�@�ΐF�̖ʐρ����F�̖ʐ�
�@�D�F�̖ʐρ��R�~�ΐF�̖ʐ�
�ł��B���̂��ƂƁA(3)����藧�̂̑̐�=875/9�p3�������̂ŁA
�@�ΐF�̖ʐρ����F�̖ʐ�=125/18�p3
�@�D�F�̖ʐρ�125/6�p3
�ƂȂ�A���ǁA�㉺�̗��̂̑̐ς�
�@125/18�p3�~8�~8�� = 125/18�p3�~64 �@���(4)
�@125/6�p3�~2�~8�� = 125/6�p3�~16 �@���(5)
�ł��B
�F�܂Ƃ�
(1)�A(2)�A(4)�A(5)���A
�@125/6�p3 �~ 24��
�@125/18�p3 �~ 72��
�ƂȂ�܂��B