問題18　（tomh　さん）　

問(1)：nxnの枠を作るのに何本の爪楊枝が必要ですか?
また、その中には1x1からnxnまで大小あわせていくつの正方形がありますか?

問(2)：3x3、4x4のそれぞれの枠で、すべての正方形を壊すには最低何本の
爪楊枝を取り除く必要がありますか?
また、その具体的な取り方も示して下さい。

３×３の正方形



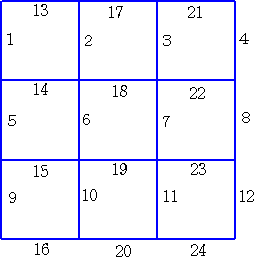
4×4の正方形


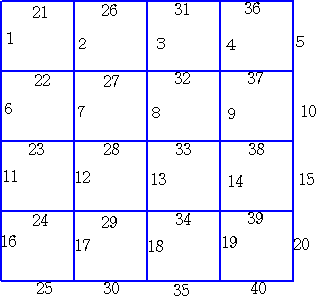
注：「正方形が壊れる」とは、その辺の一部分でも欠けるということです。
図の2x2の場合、点線が取り除いた部分です。4つの1x1の正方形のうち、
3つは辺が一つ丸々欠けて、残りの一つは二つが丸々欠けています。
そして、2x2の正方形は、右側の辺の半分が欠けていることにより
壊れた状態になっています。

(2)は問題文中、最低本数だけを尋ねていて、「最低」であることの説明（証明）は求めていませんが、
できれば証明も答えてください。（あとで送付していただいても結構です。順位には無関係です）

解答
(1) nxnの枠を作るのに必要な爪楊枝の本数は、2n(n+1) 本です。
また、nxnの枠の中に1x1の正方形は、縦にn個、横にn個並びます。
2x2の正方形は、縦にn-1個、横にn-1個並びます。…nxnの正方形は、
縦に1個、横に1個並びます。というわけで、正方形の総数は、

　Σ(k=0,n-1) (n-k)^2 = Σ(k=1,n) k^2 = n(n+1)(2n+1)/6 個

です。

(2) 正方形を壊すために取り除かなければならない爪楊枝の最低本数は、
それぞれ次のようになります（括弧内は例の図。点線が取り除いた部分）。

　3x3… 6本（図1）


　4x4… 9本（図2）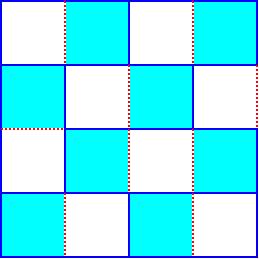

最初に4x4の枠の方から説明しましょう。
まず、4x4の枠の中にある1x1の正方形（"単位正方形"と呼んで
おきましょう）を市松模様に塗り分けます。色を付けた8個の単位正方形は、
互いに辺を共有していないので、これら8個の単位正方形を壊すには
爪楊枝を8本取り除く必要があります。同じことが色を付けていない
8個の単位正方形についてもいえます。
よって、隣り合う単位正方形の爪楊枝を取り除いて色つきと色なしの
単位正方形を"同時に"壊すことで、爪楊枝8本を取り除くことにより
16個すべての単位正方形を壊すことができます。
しかし、このとき、外枠（4x4の正方形）の辺はまったく壊れないので、
少なくとも外枠から爪楊枝を1本取り除く必要があります。
これらのことより、最低9本の爪楊枝を取り除く必要がありますが、
実際、この本数ですべて大きさの正方形を壊すことができて、一例が
図のようになります。

次に3x3の枠ですが、同じように市松模様に塗り分けます。
今度は、色つき単位正方形が、色なし単位正方形より1個多いので、
少々注意が必要です。
まず、4個の色なし単位正方形を壊すのに少なくとも4本の爪楊枝を
取り去る必要があります。このとき、同時に4個の色つき単位正方形を
壊すことにします。これは、3x3の枠内に、1x2の大きさの長方形を
4個入れることと同じです。
もし、最後の色つき単位正方形1個が、外枠と辺を共有していれば、
もう1本爪楊枝を取り除いて、この単位正方形と3x3の正方形を同時に
壊すことができて、合計5本の爪楊枝を取り除くことで目的を達成できると
思われます。
しかし、これを実行しようとしても、すべての正方形を壊すことは不可能な
ことがわかります。
よって、5本では無理なので、6本が最小数で、一例が図のようになります。

=================================================================

解答で与えた方法を素直に拡張することで、一般形が完成します。
nxnの枠を壊すには、爪楊枝を最低

　n^2 /2 +1本　（n:偶数）
　(n^2 +1) /2 +1本　（n:奇数）

取り除く必要があります。（「[]」を小数点以下切り捨ての記号とすると、
[(n^2 +3) /2]本とまとめられます）
実際に行うと、奇数の場合が図3、偶数の場合が図4となります。
それぞれの図には、枠の大きさを増やしていく手順を暗示してあります。
（正確には帰納法で示せばよいでしょう）

さて、今回は正方形だけを壊しましたが、更なるチャレンジとして、
「すべての長方形を壊す」にはどうしたらよいでしょうか?
取り除く爪楊枝の具体的な最低本数は、次のようになるそうです。

　2x2: 3, 3x3: 7, 4x4:11,
　5x5:18, 6x6:25, 7x7:34,
　8x8:43, 9x9:55, 10x10:67,
　11x11:82, 12x12:97.

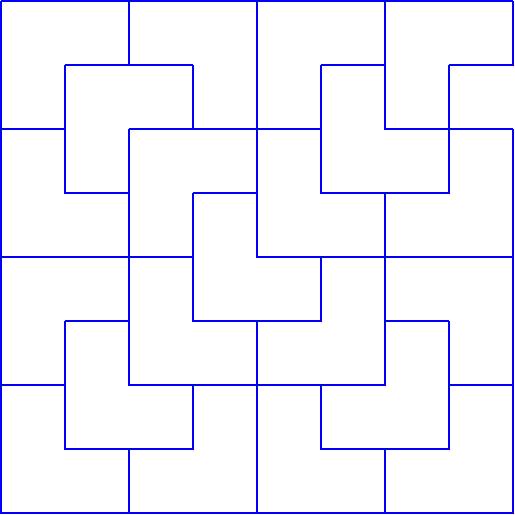
8x8の具体例を図5に示しておきます。
この発展問題、わたくし、今回も証明など一切完成しておりません。 (^^;
どなたか完成させた方は教えて下さいね。 m(__)m

=================================================================

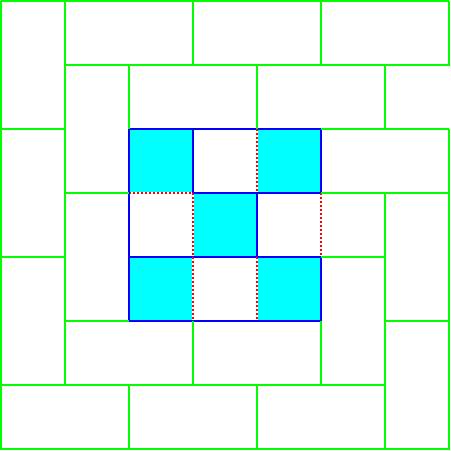
図3は最大7x7ので、



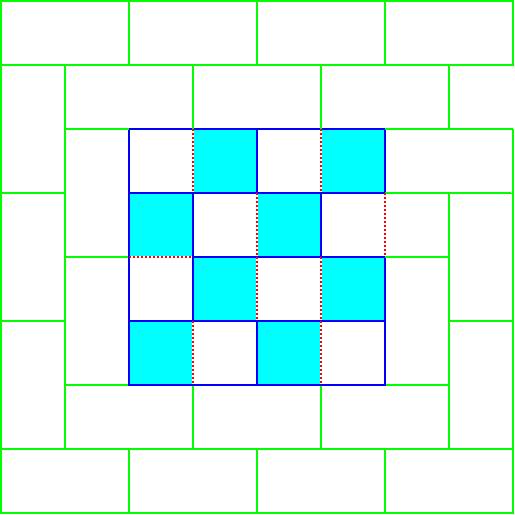
図4は最大8x8の奴です。

また、図5は大きさ8x8のL字が組合わさっている奴です。

みなさんが、「長方形破壊」を議論してくれるとうれしいなぁ。 (^0^)
「みんなで作る数学」ってのはどうですか? (^^;
一人で取り組むときと違った楽しさがありますよ。
で、名前をつけて…「ふぃぼみっち倶楽部」とかね。 (^^;;
＃決して、完成させるのをサボろうとかいうことじゃないですよ…
＃多分… ..(A^^ オイオイ、ニゲルナヨ

ではまた。