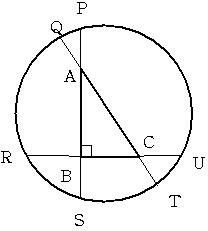
図のように周囲の長さが60cmの円があります。
この円の中に角B=90度 角A=30 度の直角三角形を描き
それぞれの辺の延長と円の交点を図のようにP,Q,R,S,T,Uとします。
弧PQの長さが4cm 弧RSの長さが10cm 弧TUの長さが8cmのとき
弧QR,弧ST,弧UPの長さを求めてください
第93回 問題 (11月5日〜12月4日) 中学生にも解けます

図のように周囲の長さが60cmの円があります。
この円の中に角B=90度 角A=30 度の直角三角形を描き
それぞれの辺の延長と円の交点を図のようにP,Q,R,S,T,Uとします。
弧PQの長さが4cm 弧RSの長さが10cm 弧TUの長さが8cmのとき
弧QR,弧ST,弧UPの長さを求めてください
解答
解1
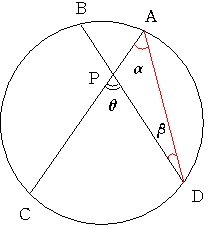
一般的に 弦ACと弦BDが円の内部点Pで交わるとき角APB=θとすると
角CAD=α 角ADB=βと置くとき θ=α+βより
弧ABと弧CDの長さの和による円周角はθとなる
よって弧の長さの和の割合は 円周の 2θ/360=θ/180となる
このことから
弧QRと弧TUの長さの和は円周の60/180=1/3
よって ST=60×1/3-8=12
弧PQと弧STの長さの和は円周の30/180=1/6
よって ST=60×1/6-4=6
弧RSと弧UPの長さの和は円周の90/180=1/2
よって ST=60×1/2-10=20
となります。
解2 算数的解法
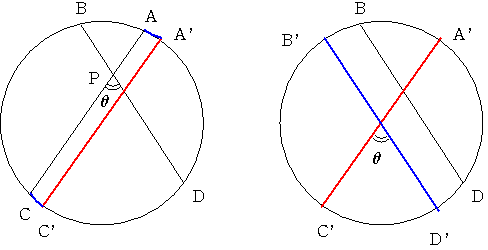
弦ABと平行に直径A'B'を描きます
AB+CD=(A'B-AA')+(CC'+C'D)=A'B+C'D
弦BDと平行に直径B'D'を描きます
A'B+C'D=(A'B'-BB')+(C'D'+D'D)=A'B'+C'D'
よってAB+CD=60×2θ/360=60×θ/180 となります
(以後 解法1と同じ)
解3 算数的解法
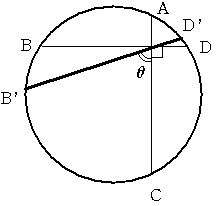
(数学問題を解いている方は算数問題を解いているものと思いますので)
算数問題の解法1により 弦AD と 弦BCが直交するとき
AD+BCは円周の1/2であることがわかります
このとき ACとB'D'のなす角がθであれば
BC:B'C=DA:D'A より (AD+BC):(AD'+B'C)=90:θ
AD'+B'Cは円周の 1/2×θ/90=θ/180 となります
(以後解法1と同じ)