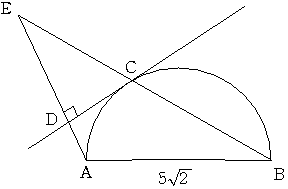
図のように直径AB=5√2である半円の弧上に点Cをとり Cでの接線にAから垂線を下ろし その足をDとします。
直線BCと直線ADの交点をEとします。
三角形ABEの面積が7であるとき 三角形CDEの面積はいくらになるでしょうか。
ただし角EABは鈍角であるとします。
第90回 問題 (7月5日〜8月4日)

図のように直径AB=5√2である半円の弧上に点Cをとり Cでの接線にAから垂線を下ろし その足をDとします。
直線BCと直線ADの交点をEとします。
三角形ABEの面積が7であるとき 三角形CDEの面積はいくらになるでしょうか。
ただし角EABは鈍角であるとします。
解答
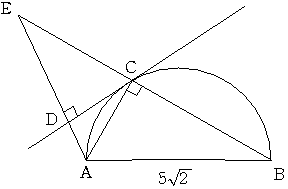
三角形ABCは直角三角形 接弦定理から 角DCA=角CBA
よって角CAE=角CAB
これより 三角形ABCと三角形AECは合同となる。
AC=x BC=yとすると 角EABが鈍角であるから x<yとなり
xy=7 x^2+y^2=(5√2)^2 から x=1 y=7
三角形CDEと三角形ABCが相似で 相似比が 5√2:7より
三角形CDEの面積は 7/2×(7/5√2)^2=343/100