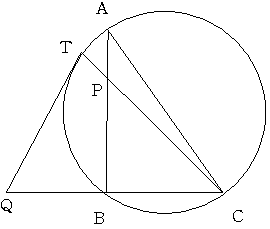
AB=8 BC=6 CA=10の直角三角形ABCの辺AB上に点PをAP=2となるようにとります。
この直角三角形の外接円と直線CPとの交点のCでないほうをTとします。
Tにおけるこの円と直線BCの交点をQとします。
TQはいくらになるでしょうか。
第86回 問題 (4月5日〜5月4日) 
AB=8 BC=6 CA=10の直角三角形ABCの辺AB上に点PをAP=2となるようにとります。
この直角三角形の外接円と直線CPとの交点のCでないほうをTとします。
Tにおけるこの円と直線BCの交点をQとします。
TQはいくらになるでしょうか。
BP=6より直角二等辺三角形BCPの斜辺PC=6√2
三角形TPBと三角形APCは相似で
TP : PB : BT = AP : PC : CA より TP : 6 : BT = 2 : 6√2 : 10 から
TP=√2 BT=5√2
三角形TBQと三角形CTQは相似で
TB : BQ : QT = CT : TQ : QC より5√2 : BQ : QT = 7√2 : TQ : (QB+6)
この式を解く
5√2 : BQ = 7√2 : TQから BQ=5/7TQ
これを BQ : QT = TQ : (QB+6) に代入すると
5/7TQ : QT = TQ : (5/7TQ+6) から
TQ=5/7(5/7TQ+6) TQ=35/4