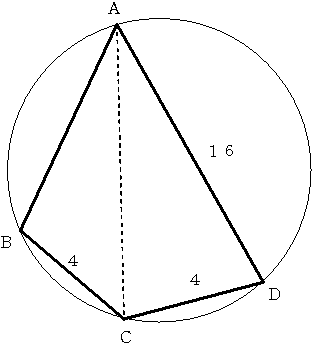
図のように、円に内接する四角形ABCDがあり BC=CD=4 DA=16となっています。
対角線AC=16のとき ABの長さはいくらになるでしょうか。
解1
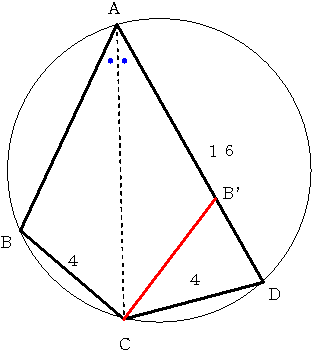
BC=CDより 円周角BAC=円周角DACとなっています。
そこでACを軸として三角形ABCを折り返すと点BはAD上の点に移動します。
その点をB'とします。
第82回 問題 (12月05日〜1月4日)
図のように、円に内接する四角形ABCDがあり BC=CD=4 DA=16となっています。
対角線AC=16のとき ABの長さはいくらになるでしょうか。

解1
BC=CDより 円周角BAC=円周角DACとなっています。
そこでACを軸として三角形ABCを折り返すと点BはAD上の点に移動します。
その点をB'とします。

このとき 三角形ACDと三角形CDB'は相似な二等辺三角形となっているので
AD:CD=CD:DB' から 16:4=4:DB' DB'=1となります
よって AB=AB'=15となります。
解2
三角形ACDで余弦定理より cos CAD= 31/32
三角形ABCで余弦定理より ABを求める。
解3
三角形ABC と三角形ACDで余弦定理を使い連立方程式を解く
cos B=-cos D を利用する