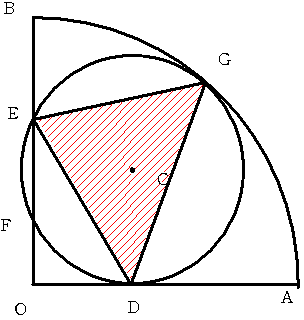
第81回　 問題　（11月12日〜12月4日）　
図のように、半径１２　中心角90度の扇形OABと、Cを中心とする半径５の円が、
２点D,Gで接し、２点E,Fで交わっています。（OE　>　OF)
このとき　三角形DEFの面積　と　三角形EDGの面積　の比を簡単な整数比で表してください。

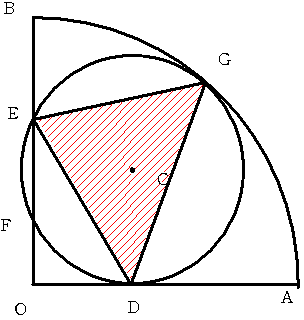
OGと点Cを中心とする円の交点のGでない方をHとします。


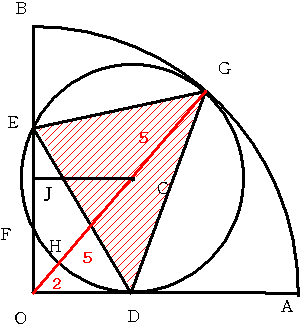
OH=OG-10=2
CからOBにおろした垂線の足をJとし　EJ=JF=ｘとすると
方べきの定理より　OH×OG=OE×OF=（OH+ｘ)(OH-x)から　2×12=(５＋ｘ）（５−ｘ）
ｘ＝１

三角形OFD=○４　とすると　三角形DEF＝○２
三角形ODC=○５

OC:CG=７：１２を使うと
三角形ODG=○５×１２／７=○６０／７
三角形EFG=三角形OED×１２／７=○６×12/7=○７２／７
三角形EDG=三角形ODG+三角形OEG-三角形ODE=○６０／７＋○７２／７−○６=○９０／７

よって　三角形DEF:三角形EDG=２：９０／７＝７：４５