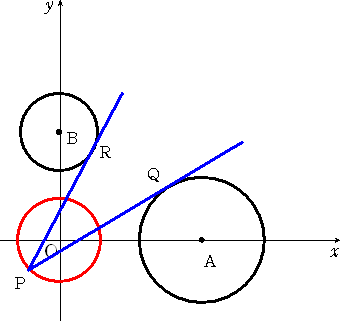
点A(8,0)を中心とする半径4の円C1 と 点B(0,6)を中心とする半径が3の円C2があります。
平面上の点P(円C1および円C2の外部の点とする)から円C1,C2へ接線を引き、
円C1、C2の接点の一つをそれぞれQ,Rとする
Pが原点を中心とし半径2の円上を動くとき PQ2+PR2 の最小値はいくらになるでしょうか
第79回 問題 (9月5日〜10月4日)
点A(8,0)を中心とする半径4の円C1 と 点B(0,6)を中心とする半径が3の円C2があります。
平面上の点P(円C1および円C2の外部の点とする)から円C1,C2へ接線を引き、
円C1、C2の接点の一つをそれぞれQ,Rとする
Pが原点を中心とし半径2の円上を動くとき PQ2+PR2 の最小値はいくらになるでしょうか

解答
三平方の定理から
PQ2+PR2= PA2-AP2 +PB2-BQ2
=PA2-16 +PB2-9
=PA2+PB2-25

ここで ABの中点(4,3)をDとし三角形PABに対して中線定理を使うと
PA2+PB2=2(PD2+AD2)=2(PD2+25)

ここで PDの最小値を考えると
PD≧OD-OP=5-2=3
よって
PQ2+PR2=PA2+PB2-25=2(PD2+25)−25=2PD2+25≧2*9+25=43
解答2
座標を使う方法