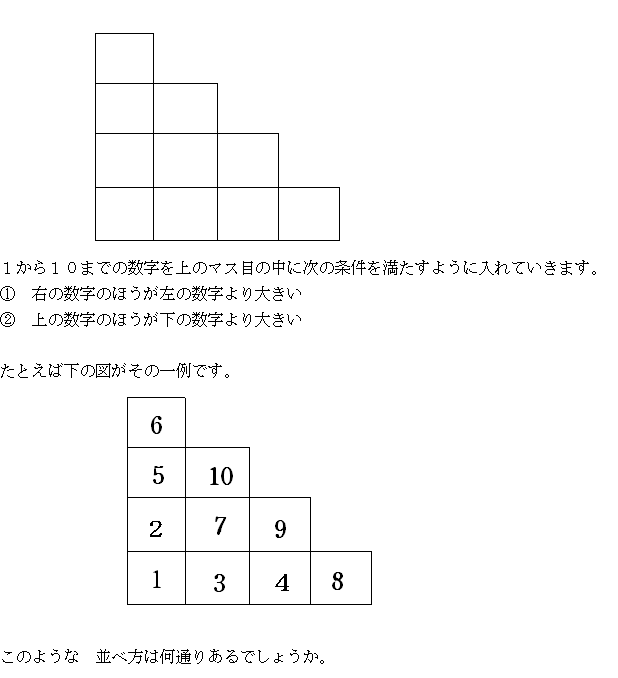
第77回　 問題　（7月5日〜8月4日）　

解答　　768

図の赤の場所の数字によって場合わけをします。
１　赤の部分が４のとき



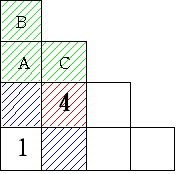
青には２，３が入るので　青の入れ方は２通り
緑の部分に数字をいれる　
　まず　のこり６つの数字から３つを選ぶ　6C3=20とおり
　その数字の一番小さいものをAにいれ　残り２つの数をB,Cに入れるので　２とおり
空白の３つの部分に数字を入れるのは　緑と同じ考え方

よって　　２×20×２×２=160通り

2　赤の部分が5のとき


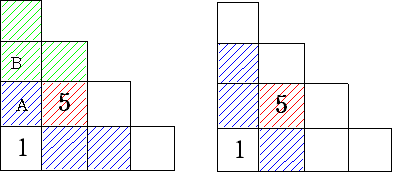
２，３，４の数字の入る場所は２通りで　図の青の部分となる
対称形であるから　前者の図形で考える。
Aに入る数字は　２，３，４のうちの１つを選ぶので３通り
　　　自動的に残りの青が決定する。
緑に入る数字を残り５つから３つ選び　5C3=10通り　Bに一番小さい数字をいれ　残りを他の緑にいれる　２通り
空白の２つの部分には　残り２つの数字を入れる　２通り
よって　２×３×10×２×２=240通り

3　赤の部分が6のとき
２，３，４，５の数字の入り方は図の青い部分となるので　３通りある

３−１の場合
青に入る２つの数字の選び方は4C2=6通り
青に数字を入れた後空白には　残りの数字が自由に入るので　4!通り
よって　6×4!=144通り

３−２の場合
２，３，４，５を　１つと３つに分けるのは　４C1＝４通り
残り４つの数から自由にAに入れる　４通り
残り３つの数から一番小さい数をBに入れ　最後の２つは自由にいれる　２通り
よって　４×４×２=32通り

３−３の場合
　　　３−２と同じ

以上から　１４４＋32＋32＝208　通り

4　赤の部分が7のとき

青い部分には　８，９，１０の数字が自由に入る
よって３×２＝６通り
残り６つの数字から　３つの数字を選んで緑の部分に入る
6C3=20通り
よって　6×20＝120通り

5　赤の部分が8のとき

青い部分には　9，１０の数字が自由に入る　２通り
残り６つの数字から　３つの数字を選んで緑の部分に入る
6C3=20通り
よって　2×20＝40通り

これらを足すと160+240+208+120+40=768　通り