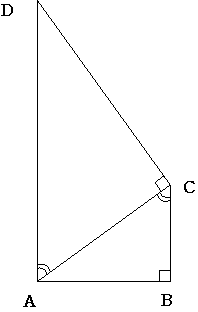
図のように∠Bを直角とする直角三角形ABCと この直角三角形に相似な直角三角形DCAを描きます。
AB=6cmのとき ADの長さの最小値はいくらになるでしょうか。
解答
第72回 問題 (2月5日〜3月4日) (中学生の範囲で解ける問題です)

図のように∠Bを直角とする直角三角形ABCと この直角三角形に相似な直角三角形DCAを描きます。
AB=6cmのとき ADの長さの最小値はいくらになるでしょうか。
解答
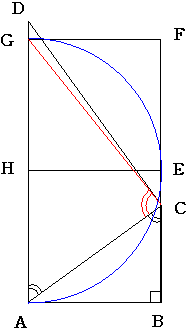
ABを一辺の長さとする正方形ABCD、正方形HEFGを描きます。また Hを中心とし、半径ABの半円を描きます。
半直線BF上にCを任意にとるとします。
CがEに一致していない時は Cは半円の外の点になっているので ∠ACGは90度より小さくなり
Dの位置は半直線AGのGより上部であることがわかります。
CがEに一致しているときは DはGに一致しています。
よってADの最小値は AG=12cmとなっています。
解答2
BCの長さをxとします。
AC=√(62+x2)
AD=AC×AC/BC= (62+x2)/x = x+36/x >= 2√(x・36/x) = 12