第70回　 問題　（12月5日〜1月4日）　（中学生のレベルの問題です）


正方形ＡＢＣＤと正方形ＰＱＲＳが同じ円に内接しています。ADとPQの交点をE　ADとPSの交点をFとします。
AP:AQ=１：√２のとき　AE:EF:FDはいくらになるでしょうか。

解答

四角形AQDPを考えます。
弦ADに対する中心角が90°ですから弦ADに対する円周角である∠AQD=45度
弦PQに対する中心角が270°ですから　弦PQに対する円周角である　∠QAP=135度となり
四角形AQDPは等脚台形であることがわかります。

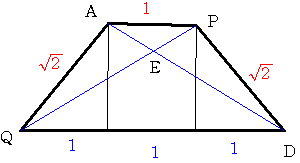
すると容易に上の青で表示した長さの比がわかりますから　三角形APEと三角形DQEが相似で相似比は1:3
よってAE:ED=1:3となります。

同様に　四角形PASDも等脚台形であることから

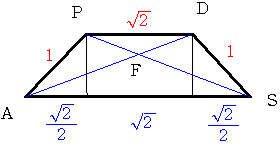
容易に上の青で表示した長さの比がわかりますから　三角形PDFと三角形SAFが相似で相似比は1:2
よって　AF:FD=2：1となります。

以上より　AE=1/4AD　FD=1/3AD　から　EF=(1-1/4-1/3)AD
AE:EF:FD=1/4:5/12:1/3=3:5:4となります