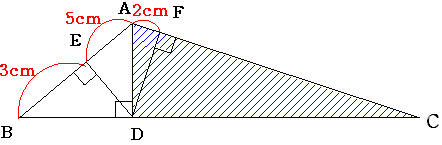
三角形ABCの頂点Aから辺BCへ下ろした垂線の足をDとし、点Dから 辺AB、辺ACへ下ろした垂線の足をE,Fとします。
AE=5cm EB=3cm AF=2cm のとき 三角形ACDの面積はいくらになるでしょうか。
図はとっても不正確です
第66回 問題 (8月6日~9月4日) 中学の知識で解けます。

三角形ABCの頂点Aから辺BCへ下ろした垂線の足をDとし、点Dから 辺AB、辺ACへ下ろした垂線の足をE,Fとします。
AE=5cm EB=3cm AF=2cm のとき 三角形ACDの面積はいくらになるでしょうか。
図はとっても不正確です
解 答
四角形AEDFについて角AED+角AFD=180度であり 向かい合った角の和が180であるから 円に内接する
よって 円周角を考え 角AEF=角ADF=90-角DAF ..①
三角形AEFと三角形ACBについて
①より 角AEF=90-角DAF=角ACB
角EAF=角CAB (同じ角)
であるから相似となり AE:AF=AC:ABから 5:2=AC:8 AC=20
FC=18である
次に三角形AFDと三角形DFCが相似であるから AF:FD=DF:FC
2:FD=FD:18 FD2=36 FD=6
よって三角形ADC=1/2×20×6=60 cm2 となります