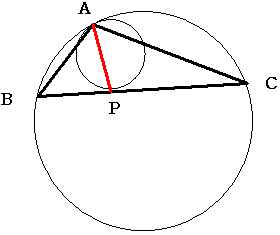
図のように 半径の異なる円が点Aで接しています。また、三角形ABCは辺BCが小さな円と接しています。
AB=2cm AC=6cmのとき APはいくらになりますか。
解答
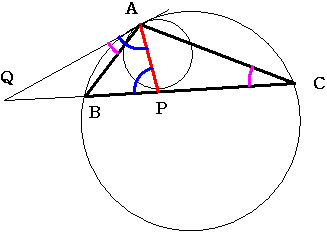
図のように点Aでの接線とBCの延長の交点をQとします。
小さい円にいして2つの接線と弦APのなす角は等しいので 角QAP=角QPA
大きい円に対して接弦定理から 角QAB=角ACB
すると 角CAP=角APB-角ACP=角QAP-角QAB=角BAP
よってAPは角BACの角の二等分線であり角BAP=角CAP=60度 であることがわかります。
三角形ABCの面積=三角形ABPの面積+三角形APCの面積ですから
2×6=2×AP+6×APから AP=3/2となります
最後のところを説明すると
S=1/2absinθを使ってもよいのですが 算数的に説明できます。
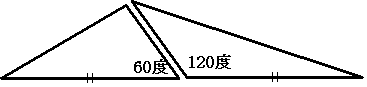
2辺の長さが等しいとき その辺のなす角が120度の三角形と 60度の三角形は面積が同じである。
これは図の三角形の面積が同じであることから わかります