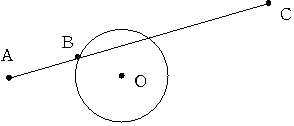
丂恾偺傛偆偵敿宎侾偺墌偲丂OA=俀丂偱偁傞揰A偑偁傝傑偡丅墌O忋偵揰B傪偲傝丂AB亊AC=12偲側傞揰C傪
敿捈慄AB忋偵偲傝傑偡丅
丂揰B偑墌O忋傪摦偔偲偒丂揰C偺昤偔恾宍偺挿偝傪媮傔偰壓偝偄丅
戞59夞丂 栤戣丂乮1寧5擔乣2寧5擔乯丂

丂恾偺傛偆偵敿宎侾偺墌偲丂OA=俀丂偱偁傞揰A偑偁傝傑偡丅墌O忋偵揰B傪偲傝丂AB亊AC=12偲側傞揰C傪
敿捈慄AB忋偵偲傝傑偡丅
丂揰B偑墌O忋傪摦偔偲偒丂揰C偺昤偔恾宍偺挿偝傪媮傔偰壓偝偄丅
夝摎

揰B偑揰P偵堦抳偡傞偲偒偺揰C傪揰Q丂揰B偑揰R偵堦抳偡傞偲偒偺揰C傪揰S偲偟傑偡丅
AP=侾傛傝丂AQ=侾俀丂丂丂AR=3傛傝丂AS=係偲側傝傑偡丅
壖掕傛傝丂AB亊AC=AP亊AQ=12
丂丂丂丂丂丂傛偭偰丂AB/AP=AQ/AC丂丂乧嘆
丂嶰妏宍ABP偲嶰妏宍AQC偵偍偄偰
丂丂丂妏BAP偲妏QAC偼摨偠妏偱偁傝
丂丂丂嘆傛傝丂偙偺妏傪嫴傓俀曈偺斾偑堦掕偱偁傞偐傜
丂丂丂仮ABP丂佷丂仮AQC
丂傛偭偰丂妏APB=妏ACQ丂丂丂乧嘇
摨條偵
壖掕傛傝丂AB亊AC=AR亊AS=12
丂丂丂丂丂丂傛偭偰丂AB/AR=AS/AC丂丂乧嘊
丂嶰妏宍ABR偲嶰妏宍ASC偵偍偄偰
丂丂丂妏BAR偲妏SAC偼摨偠妏偱偁傝
丂丂丂嘆傛傝丂偙偺妏傪嫴傓俀曈偺斾偑堦掕偱偁傞偐傜
丂丂丂仮ABR丂佷丂仮ASC
丂傛偭偰丂妏ARB=妏ACS丂丂乧嘋
仮BPR偵拝栚偡傞偲丂愒偄妏乕惵偄妏=妏PBR=90亱
傛偭偰妏ACQ偵拝栚偡傞偲丂愒偄妏乕惵偄妏=妏SCQ=90亱偲側傞
偙傟傛傝C偼SQ傪捈宎偲偡傞墌忋偵偁傞偙偲偑傢偐傞丅
SQ=AQ-AS=12-4亖8
傛偭偰丂8亊3.14=25.12