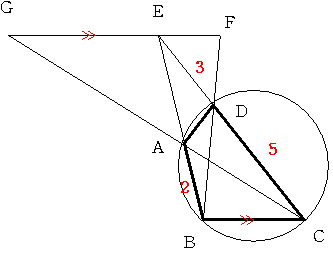
恾偺傛偆偵丂墌偵撪愙偡傞巐妏宍ABCD偑偁傝AB=俀丂CD=俆丂偲側偭偰偄傑偡丅捈慄BA偲捈慄CD偺岎揰傪
E偲偡傞偲丂DE=3偲側偭偰偄傑偡丅
E傪捠傝丂曈BC偵暯峴側捈慄偲丂懳妏慄BD偍傛傃丂懳妏慄CA偺墑挿偲偺岎揰傪偦傟偧傟F,G偲偟傑偡丅
偙偺偲偒丂AG偼DF偺壗攞偵側傞偱偟傚偆偐丅
夝摎

曽傋偒偺掕棟偐傜丂AE亊(AE+2)=3亊俉丂丂AE2+AE-24=0丂傛傝丂AE=係
仮EBC佷仮EDA傛傝丂BC:DA=6:3=2:1丂丂丏丏丏嘆
懳妏慄AC偲懳妏慄BD偺岎揰傪H偲偡傞
仮ADH佷仮BCH丂偍傛傃嘆傛傝丂AH:BH=AD:BC=1:2丂丂丏丏丏嘇
仮ABH佷DCH傛傝丂AH:DH=AB:DC=2:5丂丂丏丏丏嘊
丂丂丂丂丂丂丂丂丂丂丂丂傑偨丂HB:HC=AB:DC=2:5丂
丂丂丂丂丂丂丂丂丂丂丂丂丂嘋傛傝丂(2亊BH):HD=2:5丂偱偁傞偐傜丂AH:HC=1:5丂丂丏丏丏嘋
偡傞偲丂
仮ABC佷仮AEG傛傝丂AG:AC=AE:AB=2:4=1:2丂丂傛傝
丂AG=2AC=2(AH+HC)=2(AH+5AH)=12AH丂丂丂丂乮嘋傛傝乯
丂丂
仮BCD佷仮FED傛傝丂BD:FD=CD:ED=5:3丂丂丂傛傝
丂DF=3BD/5=3/5亊(BH+HD)=3/5亊(2AH+5/2AH)丂丂(嘇丂嘊傛傝乯
丂丂丂丂丂丂=27/10AH
傛偭偰丂AG:DF=12AH:俀俈/10AH=40:9
AG偼丂DF偺40/9攞偲側傝傑偡丅