第55回　 問題　（7月4日〜8月5日）


　
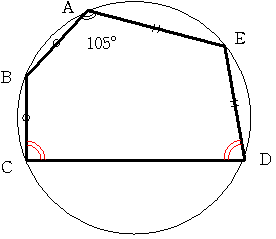
図のように円に内接する5角形があり、AB=ＢＣ　DE=EA　を満たします。角BAE=105度で角BCDと角CDEの差が25度であるとき
角BCDと角CDEのうち大きい方の角を求めてください。
（図はとっても不正確です）

解答
この問題は算数問題として考えていましたが　下の説明の(＊＊＊）のところが　算数問題としては
範囲を超えているかなあと思い　数学問題としました。たぶん算数の範囲内であると思いますが。

上の図のように　四角形BCDEを切り取ってBとE　EとBが重なるようにひっくり返してくっつけます。
Dの移った先をD'　Cの移った先をC'　とします。
すると三角形ABD'　三角形BAE　三角形C'EAはすべて合同となりますから（＊＊＊）
角ABC　角CEAは105度になります。
5角形の内角の和は　180×3=540度ですから　角D' と角C' の和は
540ー105×3=225度
差が25度ですから　大きい方の角は125度となります。

円周角の性質を使うと　角Bと角Eの和が角A の２倍であることがわかります。　これを使うと
同じように求めることができます。

最初は　角Cと角Dの和を求める問題でしたが　AB=AEとして解く方がいらっしゃると思い　問題を変形
しました。元になったのは　下にある灘の問題です。（数値は適当）。
この問題にはかなりショックを受けました。


下の6角形の面積は　長さ1の正三角形の面積の何倍か。