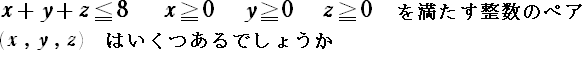
第51回　 問題　（4月5日〜5月4日）　
この問題は内容としては(小学生にはちょっとたいへんだけど）算数を使っても解ける問題です。ぜひチャレンジしてくださいね。

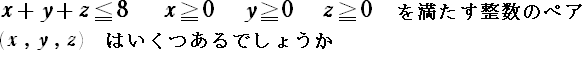
解答　1
3人の人が8個のみかんを適当に取るという問題と考えます。最初の人がとる個数をx
次の人が取る個数をy　最後の人が取る個数をzとして　残りのみかんの個数をwとすると
x+y+z≦8の整数解の個数　は　x+y+z+w=8の整数解の個数　と同じになることがわかります。

すると...　重複順列になり　○8つに　仕切り　ｌ　を3つ入れる場合の数　を求めるといいことがわかります。
そこで　11!/3!8!=165　通り　が答えであることがわかります。

解答　2

x+y+z=k-1　と仮定します(　k=1,2,...9)
zを0≦z≦k-1のある数に決定すると　x+y=k-1-zの(x,y)の解は　(0,k-1-z)　(1,k-2-z),...,(k-1-z,0)のk-z通りあります。
そこでzを0からk-1まで変化させた時の和がk-1の場合の数であり　
さらにk=1から　9まで変化させた時が全体の場合の数になるので

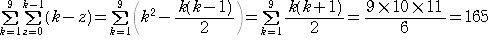
となります

解答　3

z=0のとき　x+y≦8　y=0のとき　xは9　通り　,y=1のとき　xは8通り...であるから　9+8+7+6+5+4+3+2+1=45通り
z=1のとき　x+y≦7　y=0のとき　xは8　通り　,y=1のとき　xは7通り...であるから　8+7+6+5+4+3+2+1=36通り
z=2のとき　x+y≦6　y=0のとき　xは7　通り　,y=1のとき　xは6通り...であるから　7+6+5+4+3+2+1=28通り
z=3のとき　x+y≦5　y=0のとき　xは6　通り　,y=1のとき　xは5通り...であるから　6+5+4+3+2+1=21通り　
z=4のとき　x+y≦4　y=0のとき　xは5　通り　,y=1のとき　xは4通り...であるから　5+4+3+2+1=15通り
z=5のとき　x+y≦3　y=0のとき　xは4　通り　,y=1のとき　xは3通り...であるから　4+3+2+1=10通り
z=6のとき　x+y≦2　y=0のとき　xは3　通り　,y=1のとき　xは1通り...であるから　3+2+1=6通り
z=7のとき　x+y≦1　y=0のとき　xは2　通り　,y=1のとき　xは1通りであるから　2+1=3通り　
z=8のとき　x+y≦0　y=0のとき　xは1　通り　,であるから　1通り
合計　45+36+28+21+15+10+6+3+1=　165通り