この問題は中学生程度の知識で解けます。(小学生の知識で解けないかなあ…)
図のように 正方形ABCDの辺AD CD上に PD=QDとなる点P,Qをとります。
Cを中心とし半径CDの弧とBPの交点をEとします。
角ABP=35°のとき 角DQEの大きさを求めてください。
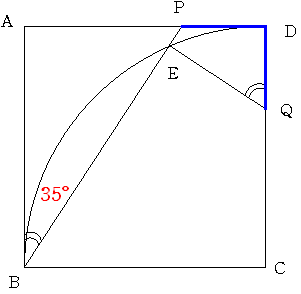
解答 55度
なかさんの解答

ほげの解答

PD=QDから AP=CQとなり 三角形ABPと三角形CBQは合同であることがわかります
よって 角APB=角CQB
次に角APB=90-35=55度 角EBC =90-35=55で 三角形BCEは二等辺三角形なので 角EBC=角CBE
よって 角APB=角CBE=角BEC
図の青い角はすべて等しいことがわかります
角BEC=角BQCであるから 四角形BCQEは円に内接していることになり 向かいあっている角の和が180度なので
角BEQ=90度であることがわかります。
すると 四角形DPEQも 角PDQ=角PEQ =90度なので 向かい合っている角の和が180度なので円に内接していることが
わかり 角EQD=角APB=55度 であることがわかります。