この問題は中学生程度の知識で解けます。
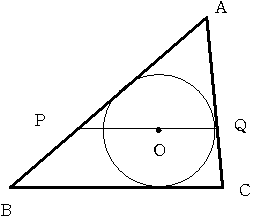
AB=11cm BC=9cm CA=7cmの三角形ABCがあります。
この三角形の内心(内接円の中心)を通りBCに平行な直線と 辺AB ACとの交点を
それぞれP,Qとします。 PQの長さを求めてください。
解答
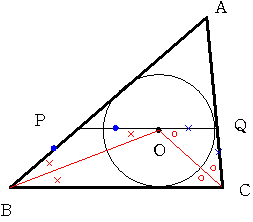
Oは内接円の中心ですから角頂点の角の二等分線の交点となっています。
PQがBCと平行であることから 三角形PBOは二等辺三角形となり、PB=PO
同様に三角形QOCも二等辺三角形となりQC=QO
三角形APQの周囲の長さはAP+PQ+QA=AP+(PO+OQ)+QA=(AP+PO)+(OQ+QA)
=(AP+PB)+(CQ+QA)=AB+AC=11+7=18
三角形ABCの周囲の長さは 11+9+7=27
三角形ABCと三角形APQは相似で相似比は 27:18=3:2となっています
よってPQ=BC×2/3=9×2/3=6 cm であることがわかります。