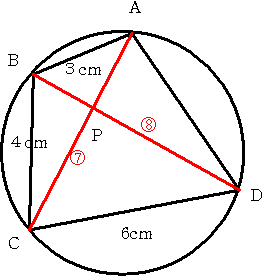
上の図のように 円に内接する四角形ABCDがあります。
AB=3cm BC=4cm CD=6cm AC:BD=7:8 のとき ADの長さはいくらになりますか。
第46回 問題 (11月5日〜12月4日)

上の図のように 円に内接する四角形ABCDがあります。
AB=3cm BC=4cm CD=6cm AC:BD=7:8 のとき ADの長さはいくらになりますか。
解答
対角線の交点をPとします。三角形ABPと三角形DCPは相似で相似比がAB:DC=1:2より
BP=xとすると CP=2xとなります。
三角形BPCと三角形APDは相似で相似比を1:kとすると AP=kx DP=2kxとなります。
AC:BD=(AP+PC):(BP+PD)=(kx+2x):(x+2kx)=(k+2):(1+2k)=7:8
よって7(2k+1)=8(k+2)から k=3/2
BCAD=4:AD=1:3/2より AD=6
注:
実際にこのような四角形は存在します。
三角形ACDがほとんど正三角形に近くなります。