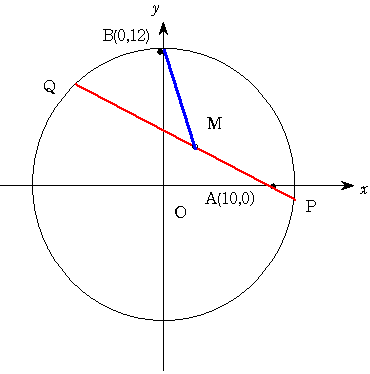
上の図のように 原点を中心とする半径12の円があります。 点A(10,0) 点B(0,12)とします。
点Aを通る直線と円の交点をP,Qとし 弦PQの中点をMとします。
BMの最小値を求めてください。
解答(浜田 明巳さん)
直線PQとx軸とのなす角をt°(0≦t<360)とし,直線PQの方程式を求め,それと円x^2+y^2=12^2との交点P,Qの座標を求める.そしてPQの中点Mの座標を求め,BMを計算し,最小値を求める.
このプログラムにより,答は8となることが分かる.
Option Explicit
Const WAKU As Double = 1
Sub Form_Load()
Picture1.Scale (-12 - WAKU, 12 + WAKU)-(12 + WAKU, -12 - WAKU)
Picture1.BackColor = vbWhite
Picture2.BackColor = vbWhite
Picture2.Picture = LoadPicture("math-045-1.gif")
Picture3.BackColor = vbWhite
End Sub
Sub Command1_Click()
On Error Resume Next
Dim Ax As Double
Dim Ay As Double
Dim Bx As Double
Dim By As Double
Dim Mx As Double
Dim My As Double
Dim Px As Double
Dim Py As Double
Dim Qx As Double
Dim Qy As Double
Dim Mxx As Double
Dim Myy As Double
Dim Pxx As Double
Dim Pyy As Double
Dim Qxx As Double
Dim Qyy As Double
Dim t As Double
Dim tt As Double
Dim t_min As Double
Dim t_max As Double
Dim t_min0 As Double
Dim t_max0 As Double
Dim a As Double
Dim b As Double
Dim aa As Double
Dim bb As Double
Dim cc As Double
Dim Dd As Double
Dim kizami As Double
Dim BM As Double
Dim min As Double
Dim dankai As Integer
Dim dankai_max As Integer
'
Ax = 10
Ay = 0
Bx = 0
By = 12
t_min0 = 0
t_max0 = 360
kizami = 0.1
min = 1000000
dankai_max = 13
For dankai = 1 To dankai_max + 1
If dankai = 1 Then
t_min = t_min0
t_max = t_max0
ElseIf dankai <= dankai_max Then
t_min = max2(tt - kizami, t_min0)
t_max = min2(tt + kizami, t_max0)
kizami = kizami * 0.1
Else
t_min = tt
t_max = tt
End If
For t = t_min To t_max Step kizami
If dankai <= dankai_max Then
If t <> 90 Then
'PQ:y=tan(t)*(x-Ax)+Ay=a*x+b
a = Tan(rad(t))
b = a * (-Ax) + Ay
'円O:x^2+y^2=12^2, PQ:y=a*x+b
'-> x^2+(a*x+b)^2=12^2 -> (1+a^2)*x^2+2*a*b*x+(b^2-12^2)=0
aa = 1 + a * a
bb = 2 * a * b
cc = b * b - 12 * 12
Dd = bb * bb - 4 * aa * cc
Px = (-bb + Sqr(Dd)) / (2 * aa)
Py = a * Px + b
Qx = (-bb - Sqr(Dd)) / (2 * aa)
Qy = a * Qx + b
Else
'PQ:x=Ax, 円O:x^2+y^2=12^2 -> Ax^2+y^2=12^2
Px = Ax
Py = Sqr(12 * 12 - Ax * Ax)
Qx = Ax
Qy = -Py
End If
Mx = (Px + Qx) * 0.5
My = (Py + Qy) * 0.5
BM = Sqr((Mx - Bx) * (Mx - Bx) + (My - By) * (My - By))
If min > BM Then
min = BM
tt = t
Mxx = Mx
Myy = My
Pxx = Px
Pyy = Py
Qxx = Qx
Qyy = Qy
Picture3.Cls
Picture3.Print "BMの最小値="; min; "(?)"
End If
Picture1.Cls
Picture1.Line (Pxx, Pyy)-(Qxx, Qyy), vbGreen
Picture1.Line (Bx, By)-(Mxx, Myy), vbGreen
Else
Mx = Mxx
My = Myy
Px = Pxx
Py = Pyy
Qx = Qxx
Qy = Qyy
Picture3.Cls
Picture3.Print "BMの最小値="; min
Picture1.Cls
End If
Picture1.Line (-12 - WAKU, 0)-(12 + WAKU, 0), vbBlack
Picture1.Line (0, -12 - WAKU)-(0, 12 + WAKU), vbBlack
Picture1.Circle (0, 0), 12, vbBlack
Picture1.Line (Px, Py)-(Qx, Qy), vbRed
Picture1.Line (Bx, By)-(Mx, My), vbBlue
Picture1.CurrentX = Ax
Picture1.CurrentY = Ay
Picture1.Print "A"
Picture1.CurrentX = Bx
Picture1.CurrentY = By
Picture1.Print "B"
Picture1.CurrentX = Mx
Picture1.CurrentY = My
Picture1.Print "M"
Picture1.CurrentX = Px
Picture1.CurrentY = Py
Picture1.Print "P"
Picture1.CurrentX = Qx
Picture1.CurrentY = Qy
Picture1.Print "Q"
Next t
Next dankai
End Sub
Sub Command2_Click()
Unload Me
End Sub
Private Function rad(ByVal x As Double) As Double
rad = 4 * Atn(1) / 180 * x
End Function
Private Function min2(ByVal x As Double, ByVal y As Double) As Double
If x < y Then
min2 = x
Else
min2 = y
End If
End Function
Private Function max2(ByVal x As Double, ByVal y As Double) As Double
If x > y Then
max2 = x
Else
max2 = y
End If
End Function
解答
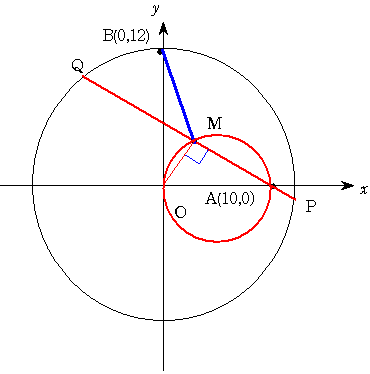
OとMをむすんでみるとMはPQの中点ですから 角OMA=90度となります。
よって MはOAを直径とする円周上にあることがわかります。
さて BMの最小値は OAの中点をC(5,0)...これは小さい円の中心です... とすると
B,M,Cが一直線上にあるときですから
BCは三平方の定理の定理から BC^2=OB^2+OC^2=12^2+5^2 BC=13
BMの最小値は 13-5=8 となります。

蛇足でしょうが B,M,Cが同一直線上にあるとき BMが最小となることを証明しておきましょう
今 C上のM以外の点をM'とします。
同一直線上にあるときは(MとM'がCに関して対称)場合は 明らかにBM<BM'です
同一直線上にないときは上の図のようになっているので 三角形の成立条件から
BM+MC<BM'+M'C MC とM'Cは半径ですから 両辺より 取り除いて
BM<BM'
よって BMの最小性が証明されました。