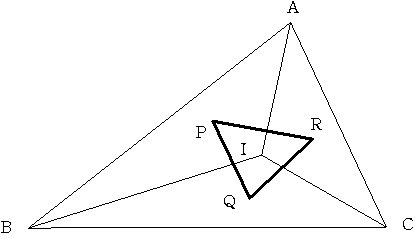
AB=10cm BC=12cm CA=8cm の三角形ABCがあります。
この三角形の内心(内接円の中心)をIとします。
三角形ABI 三角形BCI 三角形CAIの重心をそれぞれP.Q.Rとするとき
三角形PQRの辺の長さの和 PQ+QR+RP はいくらになるでしょうか。
(この問題は 中学の知識で解けます)
第39回 数学問題 (4月5日〜5月4日)
AB=10cm BC=12cm CA=8cm の三角形ABCがあります。
この三角形の内心(内接円の中心)をIとします。
三角形ABI 三角形BCI 三角形CAIの重心をそれぞれP.Q.Rとするとき
三角形PQRの辺の長さの和 PQ+QR+RP はいくらになるでしょうか。
(この問題は 中学の知識で解けます)

解答 実は三角形の内部の点は 内心I でなくても 長さは一定になります。
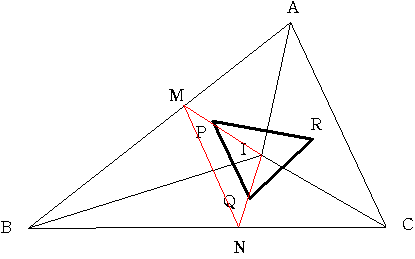
辺AB,BCの中点をM,Nとします。
三角形ABCで中点連結定理から MN=1/2ACとなります。
一方 三角形IMNにおいて IP:PM=2:1 IQ:QN=2:1ですから
三角形IMN∽三角形IPQであり 相似比は3:2ですから
PQ=2/3MN=2/3×1/2AC=1/3ACとなります。
同様にQR=1/3AB RP=1/3CBとなり
三角形PQRの周囲の長さは 三角形ABCの周囲の長さの1/3となります。
よって (10+12+8)/3=10cmであることがわかります。