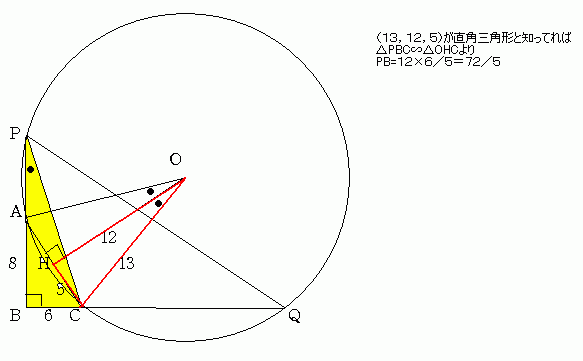
三角形ABCにおいて AB=8cm BC=6cm CA=10cm とします。
A,Cを通る半径13cmの円が BA,BCの延長線と交わる点をP,Qとします。
PQの長さはいくらでしょうか
(この問題は 中学の知識で解けます)
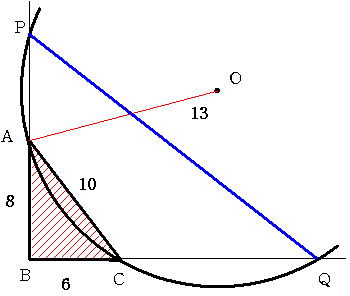
注 図は不正確です。
第38回 問題 (3月5日〜4月4日)
三角形ABCにおいて AB=8cm BC=6cm CA=10cm とします。
A,Cを通る半径13cmの円が BA,BCの延長線と交わる点をP,Qとします。
PQの長さはいくらでしょうか
(この問題は 中学の知識で解けます)

注 図は不正確です。
解答
点Pと点Cを結ぶ補助線を引く
点Rを 弧PQのうち長いほうの弧上にとる(任意) 図には描いてません

∠POQ=2×PRQ (中心角と円周角)
=2×∠PCB (四角形PCQRは 円に内接している)
∠AOC=2×角BPC (中心角と円周角)
ところが 三角形BPCは直角三角形ですから
∠PCB+∠BPC=90°
よって ∠POQ+∠AOC=180°となります。
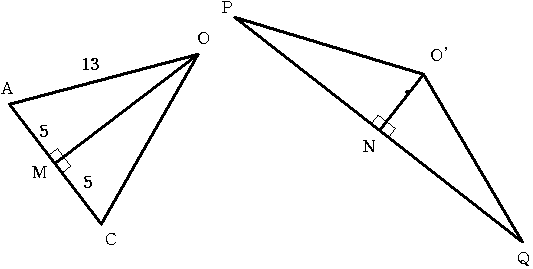
そこで 2つの2等辺三角形OAC と O'PQを抜き出し 頂点から 対辺へ垂線OM O'Nを
下ろすと ∠AOM+∠PO'N=180°から 上の4つの三角形はすべて合同であることが
わかりますから PQ=2×OM= 2×12=24 cmとなります。
解答 ろろさん
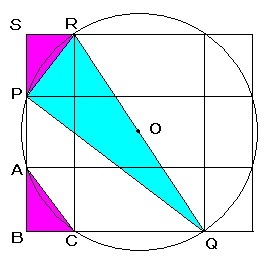
図のような格子を描きこみ△ABC≡△PSRより
PR=10cm
RQ=26cm
△RPQは直角三角形なので
PQ=12x2=24
解答 なかさん

解答 miyaさん