第37回　 問題　（2月5日〜3月4日）
一辺が24cmの正三角形ABCの頂点A,Cに点P,Qがあり、点Pは辺AB上をAからBへ　点Qは辺CA上をＣからAへ
同じ速さで移動します。このとき　点Rを三角形PQRが正三角形になるようにとります。（Rは直線PQの上部にある
ものとします）　P.Qが移動を終了したとき　Rの描く図形の線の長さを求めてください。



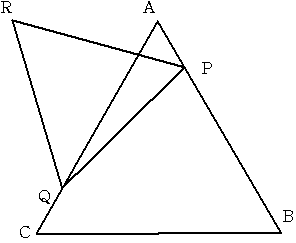
注　図は不正確です。

解答



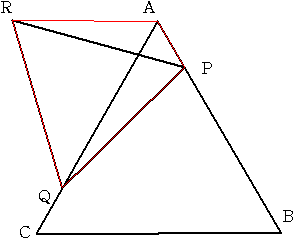
四角形ARQP　について考えると　角QAP=角QRP（=60度）より
四角形ARQPは円に内接することがわかります。
すると角RAQ=角RPQ=60度ということがわかります。

このことから　角RAC=角ACB=60度であり　ARとBCは平行であることがわかります

Rは上の図の赤い実線部分を移動することがわかりますので軌跡の長さは48cmであることがわかります。