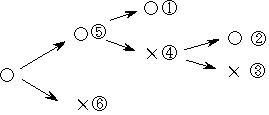
戞36夞丂 栤戣丂乮1寧5擔乣2寧4擔乯
N偝傫丂偲丂Y偝傫偑丂偍屳偄400墌偯偮弌偟偰丂僎乕儉傪巒傔傑偟偨丅彑偭偨傎偆偑偡傋偰偺丂偍嬥傪傕傜偊傞偲偄偆傢偗偱偡丅
偲偙傠偑丂N偝傫偑丂侾彑偟偨偲偙傠偱僎乕儉傪拞抐偡傞偼傔偵側傝傑偟偨偺偱丂偍屳偄偑弌偟偨偍嬥傪丂偦偺応偱暘偗傞偙偲偵側傝傑偟偨丅
偍屳偄偑晄暈偺側偄傛偆偵暘偗傞帪丂N偝傫偑庴偗庢偭偨嬥妟傪師偺俀偮偺傛偆側僎乕儉傪偟偨応崌偵偮偄偰摎偊偰偔偩偝偄丅
(1)丂愭偵3彑偟偨傎偆偑丂彑偪偲偟偰丂偍嬥傪偡傋偰傕傜偊傞傛偆側僎乕儉偺応崌丂丂丂偨偲偊偽丂俁彑俀攕偵側偭偨傜傕傜偊傞
(2)丂彑攕偱俆偮偺嵎偑偮偄偨偲偒偵丂偍嬥傪偡傋偰傕傜偊傞傛偆側僎乕儉偺応崌丂丂丂偨偲偊偽100彑95攕偵側偭偨傜傕傜偊傞
偨偩偟丂偙偺僎乕儉傪1夞偡傞偲偒丂N偝傫偲丂Y偝傫偺彑偮妋棪偼丂摨偠傕偺偲偟傑偡丅
丂
(侾)偺夝摎
彑偪傪仜晧偗傪亊偱偁傜傢偟傑偡
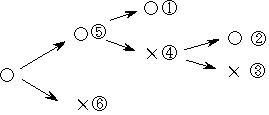
偙偺偁偲帋崌傪偮偯偗偨偲偡傞偲
丂丂嘆偺忬懺偱偼丂摉慠800墌偑N偝傫偺傕偺偵側傝傑偡丅
丂丂嘇偺忬懺偱傕偦偆偱偡丂
丂丂嘊偵側傞偲俀彑俀晧側偺偱丂尦嬥傪400墌偯偮暘偗偰廔椆偵側傝傑偡丅
丂丂偦偆偡傞偲丂嘋偺偲偒偵偼丂嘇偲嘊偺暯嬒偺(800+400)/2傪N偝傫偑庴偗庢傞偙偲偵側傝傑偡丅乧乧側偤暯嬒偵偡傞偲傛偄偐偼屻傠偺夝愢傪尒偰偔偩偝偄
丂丂摨條偵嘍偱偼丂嘆偲嘋偺暯嬒偱丂(800+600)/2=700墌傪N偝傫偑庴偗庢傝傑偡丅
丂丂嘐偱偼侾彑侾攕側偺偱丂400墌偯偮暘偗傑偡偹
丂偱偡偐傜丂尰嵼偼丂嘍偲嘐偺暯嬒偺丂(400+700)/2=550墌傪N偝傫偑庴偗庢傞偲傛偄傢偗偱偡丅
暯嬒傪峫偊傞偲傛偄傢偗
丂嘋偺忬懺偵側偭偨偲偟傑偡丅N偝傫偵偮偄偰峫偊傑偟傚偆丅
丂傕偟丂N偝傫偑彑偮偲800墌傕傜偄丂晧偗傞偲400墌傕傜偆偙偲偵側傝傑偡丅偡傞偲丂N偝傫偼丂偳偪傜偵偟偰傕400墌偼傕傜偆偙偲偵側傞偺偱
丂愭偵400墌傪暐偭偰偍偒傑偟傚偆丅
丂偡傞偲嘋偺忬懺偱丂N偝傫偼丂彑偮偲400墌傕傜偄丂晧偗傞偲0墌偵側傝丄Y偝傫偼彑偮偲400墌傕傜偄丂晧偗傞偲0墌偵側傞偙偲偵側傝傑偡丅
丂偲偄偆偙偲偼丂嘋偺忬懺偱偍屳偄200墌傪弌偟崌偄丂400墌傪偐偗偰侾夞彑晧傪偟偰傞偙偲偲摨偠偱偡丅
丂偱偡偐傜丂嘋偺忬懺偱傗傔傞帪偼丂N偝傫偼丂400墌+200墌=600墌丂傕傜偄丂Y偝傫偼丂200墌傕傜偭偰彑晧傪偟側偄丂偲偄偆偺偑丂夝寛埬偱偡丅
丂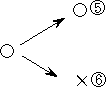
傛傝堦斒揑偵丂a墌傪彑偮偲N偝傫偑丂彑偮偲x墌傕傜偄晧偗傞偲倷墌傕傜偆偲偟傑偡乮x>y)
丂N偝傫偼丂偳偆偣y墌偼栣偆偺偱愭偵傕傜偭偪傖偄傑偡丅
Y偝傫偼丂彑偮偲(a-y)墌傕傜偄丂晧偗傞偲(a-x)墌傕傜偄傑偡丅丂
丂Y偝傫偼偳偆偣丂(a-x)墌偼傕傜偆偺偱丂偝偒偵傕傜偭偪傖偄傑偡丅
偡傞偲偙偺僎乕儉偼丂N偝傫偵偲偭偰偼彑偮偲丂(x-y)墌傕傜偄丂傑偗傞偲0墌傕傜偆僎乕儉偵側傝傑偡
丂丂丂丂丂丂丂丂丂丂丂丂丂Y偝傫傫偄偲偭偰偼丂彑偮偲丂(a-y)-(a-x)=(x-y)墌傕傜偄丂晧偗傞偲0墌傕傜偆僎乕儉偵側傝傑偡丅
偲偄偆偙偲偼丂乮倶亅y)墌偺僎乕儉傪巒傔傞悺慜偱僎乕儉傪傗傔傞偙偲偲摨偠偱偡偐傜丂偙傟傪摍暘偟偰傢偗偰丂僎乕儉傪偟側偄
偲偄偆偺偑堦斣偺夝寛嶔偱偡丅
偲偄偆偙偲偱丂N偝傫偺傕傜偆嬥妟偼丂y+(x-y)/2=(x+y)/2丂Y偝傫偺傕傜偆嬥妟偼丂(a-x)+(x-y)/2=a-(x+y)/2偲側傝傑偡
偮傑傝丂忋偺恾偺嘍偲嘐偺暯嬒偲側傞傢偗偱偡丅
(2)偺夝摎
偙偺僎乕儉偼丂400/5=80墌傪侾夞偺彑晧偑偒傑傞偮偳偍屳偄偵傗傝庢傝偡傞偲偄偆僎乕儉偲摨偠偱偡丅
俆偮偺嵎偑偱偒偨帪偵丂400墌偺帩偪嬥偑側偔側偭偰偍傢傞偲偄偆偩偗偺榖偱偡丅
偱偡偐傜丂N偝傫偑侾夞彑偭偨偲偄偆偙偲側偺偱丂N偝傫偑80墌栕偗偰傞偲偄偄傢偗偱偡偐傜丂N偝傫偺庴偗庢傞嬥妟偼480墌偱偡丅

傛傝徻偟偄夝愢
偍屳偄偍嬥傪弌偡偺偱偼側偔憡庤偐傜
嘆偺忬嫷偱a墌庴偗庢傞偲偟傑偡
嘇偺忬嫷偱偼侾彑侾攕偱偡偐傜侽墌庴偗庢傝傑偡丅
嘊偱偼丂丂忋偱夝愢偟偨傛偆偵丂嘆=(嘇+嘊)/俀傛傝丂丂嘊=2亊嘆-嘇偱偡偐傜丂嘊=2亊a-0=2a墌庴偗庢傝傑偡
嘋偱偼丂俀彑侾攕側偺偱丂1彑0攕偲摨偠忬嫷偱偡丅傛偭偰嘋=嘆=a
嘍偱偼丂嘊=(嘋+嘍)/2傛傝丂嘍=2亊嘊-嘋=2亊2a-a=3a
嘐偱偼丂3彑侾攕側偺偱丂2彑0攕偲摨偠忬嫷偱偡丅傛偭偰丂嘐=嘊=2a
嘑偱偼丂嘍=(嘐+嘑)/2傛傝丂嘑=2亊嘍-嘐=2亊3a-2a=4a
嘒偱偼丂4彑侾攕側偺偱丂3彑0攕偲摨偠忬嫷偱偡丅傛偭偰丂嘒=嘍=3a
嘓偱偼丂嘑=(嘒+嘓)/2傛傝丂嘓=2亊嘑-嘒=2亊4a-3a=5a
嘓偺忬嫷偱俆彑偟偨偺偱400墌庴偗庢傞
偮傑傝丂5a=400偐傜丂a=80墌偲偄偆偙偲偑傢偐傝傑偡丅
栤戣暥偺儖乕儖偩傠400墌偩偟偨偺偱丂480墌庴偗庢傞偲偄偆偙偲偱偡
偨偲偊偽嘍偺忬嫷傪峫偊傞偲傛偔傢偐傞偑嘐偲嘑偺暯嬒偑嘍偦偟偰嘐偵側傞偙偲偲丂偦偺慜偺嘊偵側傞偙偲偑摨偠
偮傑傝嘊偲嘑偺暯嬒偑嘍偲偄偆偙偲偵側傝傑偡丅丂偮傑傝丂嘊嘍嘑偼摍嵎悢楍偵側偭偰偄傞偙偲偑傢偐傝傑偡丅
偱偡偐傜丂偙偺彑晧偺悢帤偑5彑偺嵎偱傕10彑偺嵎偱傕摨偠傛偆偵寁嶼偱偒傞偙偲偑傢偐傝傑偡丅
偙偺(2)偺傛偆側栤戣傪擖帋偱偼尒偐偗側偄偺偱丂偳偆偟偰偩傠偆偲巚偭偨傜丂忋偺傛偆側寢壥偵側傝傑偟偨丅
偩偐傜擖帋偱偼弌側偄傫偩丂偲偄偆偙偲傪抦傝傑偟偨乮曌嫮晄懌乧乯
(1)偼婜懸抣偺栤戣偵側傞偺偱丂妋棪傪弌偟偰傕偱偒傞偺偱偡偑丂偦傟偼奆偝傫偵偍擟偣偟傛偆偐側偁丂偲乧丅