��34��@ ����@�i11��5���`12��4���j

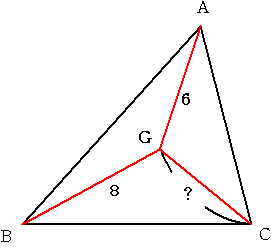
�@3�p�`ABC�̏d�S��G�Ƃ��܂��@�}�̂悤�Ɂ@AG=�Ucm�@BG=�Wcm�ł���
�܂��@AB�~AB+BC�~BC�{CA�~CA=492cm^2�@�ƂȂ��Ă��܂��B
���̂Ƃ��@CG�̒��������߂Ă��������B�@
���@

AG,BG,CG��������BC.CA.AB�ƌ����_��L,M,N�Ƃ��܂��B
G�͏d�S�ł�����@AL=�X�@BM=�P�Q�ƂȂ�܂��B
�܂�G�͏d�S�ł�����@L,M,N��BC,CA,AB�̒��_�ɂȂ��Ă��܂��B
�����藝����
�@�@AB^2+AC^2=2(AL^2+BL^2)�@����ā@AB^2+AC^2=2 (81+BC^2/4) �c�c�@
�@�@BC^2+AB^2=2(BM^2+CM^2)�@����ā@BC^2+AB^2=2 (144+AC^2/4) �c�c�A
�@�@AC^2+BC^2=2(CN^2+AN^2)�@����ā@AC^2+BC^2=2 (CN^2+AB^2/4) �c�c�B
�@�A�B�𑫂��Ɓ@�@�@�Q(AB^2+BC^2+CA^2)=�Q(CN^2+225+(AB^2+BC^2+CA^2)/4)
�@���ӂ��Q�Ŋ���AB^2+BC^2+CA^2=492�������ā@�@
�@�@�@�@�@�@�@�@�@�@�@�@492=CN^2+225+123���
�@�@�@�@�@�@�@�@�@�@�@�@CN^2=144
�@�@�@�@�@�@�@�@�@�@�@�@CN=12
�@�@�@�@�@�@�@�@�@�@�@�@CG=12�~2/3=�W
���̂悤�ȎO�p�`�����݂��邱�Ƃ́@�@��
AB^2+CA^2=492-BC^2�������ā@BC�����߁@�O�p�`�̐��������������Ƃ�
���ׂ邱�ƂɂȂ�܂��B
�������@���݂��邱�Ƃ��m�F�ł��܂��B�i�ȗ��j
�@