第33回　 問題　（10月5日〜11月4日）

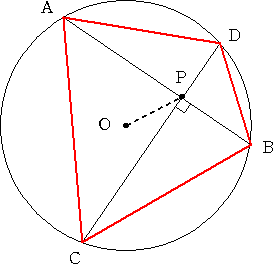
半径5cmの円の中心をOとします。中心Oから3cmはなれた点をPとします。
Pを通り直交する円の２つの弦　ABとCD　を引きます。
このとき　四角形ACBDの面積の最大値と最小値を求めてください。

（この問題は中学の数学の知識を必要とします）



まず　AB＾2+CD^2を求めます。
上の図のように　OからAB,CDに垂線を下ろし　垂線の足をF,Eとします。

　AB^2+CD^2
=(2AF)^2+(2CE)^2
=4(OA^2-OF^2)+４(OC^2-OE^2)
=4(25+25)-4(OF^2+OE^2)　　　　　　OA=OC=半径５　　
=200-4×OP^2　　　　　　　　　　　　OF^2+OE^2=OF^2+FP^2=OP^2
=200-4×9=164

つぎに　AB^2+CD^2=(AB-CD)^2+2×AB×CD　であるから
求める面積をS=1/2×AB×CDとすると、
　(AB-CD)^2+2×AB×CD=AB^2+CD^2=164
　4S=164-(AB-CD)^2となる。

よってAB-CD=0のとき　Sは最大値で　4S=164から　S=41
　　実際　下図のようにOPを通る直径に対しAB　CDが45度の角度になるとき
　　明らかにAB=CDになります



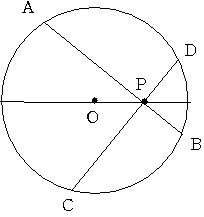
AB　とCDの差が最大になるときにSは最小になりますが
　　点Pを通る弦の長さが最大になるのはOPを通る直径であり　
　最小になるのはOPを通る直径に垂直な弦であることは明らかでしょう
　（弦と中心の距離が小さいほど　三平方の定理から　弦の長さが長くなります）

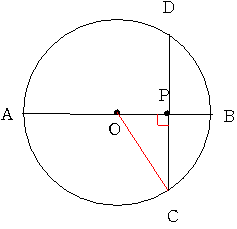
　ABが最大の長さである直径のとき　CDは最小の長さである弦になりますから
　このとき　(AB-CD)^2は最大になります（逆のときもそうです）
つまり　このとき　Sが最小になります。
　AB=10のときCDは　CD^2=(2CP)^2=４（OC^2-OP^2)=4(25-9)=64
CD=８となります　よって　S=1/2×10×8=40　となります。

以上から面積の最大値は　41cm^2　最小値は　40cm^2であることがわかります。


最大　と　最小の　面積の差って　思ったよりないなあ　という感じがしました。


解答２　浜田　明巳さん


　ＶＢで解きました．（http://micci.sansu.org/zukei/math-033/　からダウンロードできます）

　最大値は４１cm2，最小値は４０cm2です．あまり差がないようですね．

Option Explicit
Const R As Double = 5
Sub Form_Load()
Dim waku As Double
waku = R * 0.2
Picture1.Scale (-R - waku, R + waku)-(R + waku, -R - waku)
Picture1.BackColor = vbWhite
Picture2.BackColor = vbWhite
Picture2.Picture = LoadPicture("math-033-1.gif")
Picture3.BackColor = vbWhite
End Sub
Sub Command1_Click()
Dim Ax As Double
Dim Ay As Double
Dim Bx As Double
Dim By As Double
Dim Cx As Double
Dim Cy As Double
Dim Dx As Double
Dim Dy As Double
Dim Px As Double
Dim Py As Double
Dim Axx1 As Double
Dim Ayy1 As Double
Dim Axx2 As Double
Dim Ayy2 As Double
Dim Bxx1 As Double
Dim Byy1 As Double
Dim Bxx2 As Double
Dim Byy2 As Double
Dim Cxx1 As Double
Dim Cyy1 As Double
Dim Cxx2 As Double
Dim Cyy2 As Double
Dim Dxx1 As Double
Dim Dyy1 As Double
Dim Dxx2 As Double
Dim Dyy2 As Double
Dim At As Double
Dim Att As Double
Dim At_min As Double
Dim At_max As Double
Dim kizami As Double
Dim menseki As Double
Dim max As Double
Dim min As Double
Dim a As Double
Dim b As Double
Dim c As Double
Dim d As Double
Dim aa As Double
Dim bb As Double
Dim cc As Double
Dim Dd As Double
Dim x(1) As Double
Dim y(1) As Double
Dim AB(1) As Double
Dim CD As Double
Dim gosa As Double
Dim ten_hankei As Double
Dim j As Integer
'
Px = 3
Py = 0
kizami = 0.05
At_min = 0
At_max = 180
max = 0
min = 10000
gosa = 10 ^ (-15)
ten_hankei = 0.02
For At = At_min To At_max Step kizami
If At = 0 Then
Ax = R
Ay = 0
Bx = -R
By = 0
Cx = 3
Cy = Sqr(R * R - Cx * Cx)
Dx = 3
Dy = -Cy
ElseIf At = 180 Then
Ax = -R
Ay = 0
Bx = R
By = 0
Cx = 3
Cy = -Sqr(R * R - Cx * Cx)
Dx = 3
Dy = -Cy
Else
Ax = R * Cos(radians(At))
Ay = R * Sin(radians(At))
If Abs(Ax - Px) > gosa Then
'AP:y=(Py-Ay)/(Px-Ax)*(x-Ax)+Ay=a*x+b
a = (Py - Ay) / (Px - Ax)
b = a * (-Ax) + Ay
'x^2+y^2=5^2 -> x^2+(a*x+b)^2=5^2 -> aa*x^2+bb*x+cc=0
aa = 1 + a * a
bb = 2 * a * b
cc = b * b - R * R
Dd = bb * bb - 4 * aa * cc
For j = 0 To 1
x(j) = (-bb + (1 - j * 2) * sqrt(Dd)) / (2 * aa)
y(j) = a * x(j) + b
AB(j) = sqrt((x(j) - Ax) * (x(j) - Ax) + (y(j) - Ay) * (y(j) - Ay))
Next j
j = -(AB(0) < AB(1))
Bx = x(j)
By = y(j)
'CD:y=-1/a*(x-Px)+Py=c*x+d
c = -1 / a
d = c * (-Px) + Py
'x^2+y^2=5^2 -> x^2+(c*x+d)^2=5^2 -> aa*x^2+bb*x+cc=0
aa = 1 + c * c
bb = 2 * c * d
cc = d * d - R * R
Dd = bb * bb - 4 * aa * cc
For j = 0 To 1
x(j) = (-bb + (1 - j * 2) * sqrt(Dd)) / (2 * aa)
y(j) = c * x(j) + d
Next j
'C:直線ABにおいて,原点と同じ側にある
j = -(Sgn(a * x(0) - y(0) + b) * Sgn(a * 0 - 0 + b) < 0)
Cx = x(j)
Cy = y(j)
Dx = x(1 - j)
Dy = y(1 - j)
Else
'AP:x=Px=3
'x^2+y^2=5^2 -> y^2=5^2-x^2
Bx = Px
By = -sqrt(R * R - Bx * Bx)
Cx = -R
Cy = 0
Dx = R
Dy = 0
End If
End If
AB(0) = sqrt((Bx - Ax) * (Bx - Ax) + (By - Ay) * (By - Ay))
CD = sqrt((Dx - Cx) * (Dx - Cx) + (Dy - Cy) * (Dy - Cy))
menseki = AB(0) * CD * 0.5
If max < menseki Then
max = menseki
Axx1 = Ax
Ayy1 = Ay
Bxx1 = Bx
Byy1 = By
Cxx1 = Cx
Cyy1 = Cy
Dxx1 = Dx
Dyy1 = Dy
End If
If min > menseki Then
min = menseki
Axx2 = Ax
Ayy2 = Ay
Bxx2 = Bx
Byy2 = By
Cxx2 = Cx
Cyy2 = Cy
Dxx2 = Dx
Dyy2 = Dy
End If
Picture3.Cls
Picture3.Print "四角形ACBDの最大値(緑)="; max; "cm2(?), 最小値(青)="; min; "cm2(?)"
Picture1.Cls
Picture1.Line (Axx1, Ayy1)-(Cxx1, Cyy1), vbGreen
Picture1.Line -(Bxx1, Byy1), vbGreen
Picture1.Line -(Dxx1, Dyy1), vbGreen
Picture1.Line -(Axx1, Ayy1), vbGreen
Picture1.Line -(Bxx1, Byy1), vbGreen
Picture1.Line (Cxx1, Cyy1)-(Dxx1, Dyy1), vbGreen
Picture1.Line (Axx2, Ayy2)-(Cxx2, Cyy2), vbBlue
Picture1.Line -(Bxx2, Byy2), vbBlue
Picture1.Line -(Dxx2, Dyy2), vbBlue
Picture1.Line -(Axx2, Ayy2), vbBlue
Picture1.Line -(Bxx2, Byy2), vbBlue
Picture1.Line (Cxx2, Cyy2)-(Dxx2, Dyy2), vbBlue
Picture1.Circle (0, 0), 5, vbBlack
Picture1.Line (Ax, Ay)-(Cx, Cy), vbRed
Picture1.Line -(Bx, By), vbRed
Picture1.Line -(Dx, Dy), vbRed
Picture1.Line -(Ax, Ay), vbRed
Picture1.Line -(Bx, By), vbBlack
Picture1.Line (Cx, Cy)-(Dx, Dy), vbBlack
Picture1.Line (0, 0)-(Px, Py), vbBlack
Picture1.Circle (0, 0), ten_hankei, vbBlack
Picture1.CurrentX = Ax
Picture1.CurrentY = Ay
Picture1.Print "A"
Picture1.CurrentX = Bx
Picture1.CurrentY = By
Picture1.Print "B"
Picture1.CurrentX = Cx
Picture1.CurrentY = Cy
Picture1.Print "C"
Picture1.CurrentX = Dx
Picture1.CurrentY = Dy
Picture1.Print "D"
Picture1.CurrentX = Px
Picture1.CurrentY = Py
Picture1.Print "P"
Picture1.CurrentX = 0
Picture1.CurrentY = 0
Picture1.Print "O"
Next At
Picture3.Cls
Picture3.Print "四角形ACBDの最大値(緑)="; max; "cm2, 最小値(青)="; min; "cm2"
Picture1.Cls
Picture1.Circle (0, 0), 5, vbBlack
Picture1.Line (Axx1, Ayy1)-(Cxx1, Cyy1), vbGreen
Picture1.Line -(Bxx1, Byy1), vbGreen
Picture1.Line -(Dxx1, Dyy1), vbGreen
Picture1.Line -(Axx1, Ayy1), vbGreen
Picture1.Line -(Bxx1, Byy1), vbGreen
Picture1.Line (Cxx1, Cyy1)-(Dxx1, Dyy1), vbGreen
Picture1.Line (Axx2, Ayy2)-(Cxx2, Cyy2), vbBlue
Picture1.Line -(Bxx2, Byy2), vbBlue
Picture1.Line -(Dxx2, Dyy2), vbBlue
Picture1.Line -(Axx2, Ayy2), vbBlue
Picture1.Line -(Bxx2, Byy2), vbBlue
Picture1.Line (Cxx2, Cyy2)-(Dxx2, Dyy2), vbBlue
Picture1.Line (0, 0)-(Px, Py), vbBlack
Picture1.Circle (0, 0), ten_hankei, vbBlack
Picture1.CurrentX = Axx1
Picture1.CurrentY = Ayy1
Picture1.Print "Amax"
Picture1.CurrentX = Bxx1
Picture1.CurrentY = Byy1
Picture1.Print "Bmax"
Picture1.CurrentX = Cxx1
Picture1.CurrentY = Cyy1
Picture1.Print "Cmax"
Picture1.CurrentX = Dxx1
Picture1.CurrentY = Dyy1
Picture1.Print "Dmax"
Picture1.CurrentX = Axx2
Picture1.CurrentY = Ayy2
Picture1.Print "Amin"
Picture1.CurrentX = Bxx2
Picture1.CurrentY = Byy2
Picture1.Print "Bmin"
Picture1.CurrentX = Cxx2
Picture1.CurrentY = Cyy2
Picture1.Print "Cmin"
Picture1.CurrentX = Dxx2
Picture1.CurrentY = Dyy2
Picture1.Print "Dmin"
Picture1.CurrentX = Px
Picture1.CurrentY = Py
Picture1.Print "P"
Picture1.CurrentX = 0
Picture1.CurrentY = 0
Picture1.Print "O"
End Sub
Sub Command2_Click()
Unload Me
End Sub
Private Function sqrt(ByVal x As Double) As Double
If x <= 0 Then
sqrt = 0
Else
sqrt = Sqr(x)
End If
End Function
Private Function radians(ByVal x As Double) As Double
radians = 4 * Atn(1) / 180 * x
End Function