第31回　 問題　（7月5日〜8月4日）

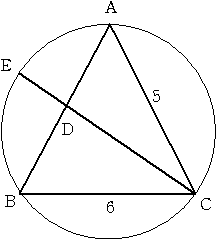
二等辺三角形ABCがあり、AB=AC=５cm　BC=６cmとなっています。
この三角形の外接円のひとつの直径をCEとします。
CEとABの交点をDとするとき　CD:DEを簡単な整数比で表してください。

解答

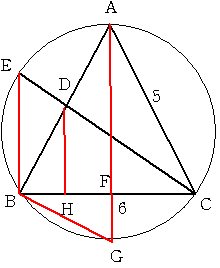
図のようにAからBCに垂線を下ろしその足をFとします
またDから辺BCに垂線を下ろし、足をHとします。（別解で使用します）
AFの延長線と円の交点をGとします。明らかにAGは直径となります。

１　直径の長さ
　三角形ABFは3:4:5の直角三角形です。
　これは直角三角形ABGと相似ですから　AB:AG=4:5　よってAG=5×5/4=25/4となります。
　　
　別解
　　方べきの定理から　BF×FC=AF×FG　よって　３×３=４×FG　　FG=9/4
　　よって直径は4+9/4=25/4
　
2　BEの長さ
　三角形BCEは直角三角形ですから　三平方の定理から
　BE=√(25/4)^2-6^2=7/4
　　
　別解
　円の中心をOとするとOF=25/8-9/4=7/8
　三角形COFと三角形CEBは相似なので　EB=7/4　

３　答
　CD:DE=三角形ABC:三角形ABE=1/2×6×4:1/2×7/4×3=32:7

別解
２までは上と同じ
3　BHの長さ
　三角形BDHは3:4:5の直角三角形なので　BH=3x　DH=4xとすると
　三角形CDHと三角形CEBが相似なので
　　CH:HD=CB:BEから　(6-3x):4x=6:7/4　　x=14/39　BH=3x=42/39
４　　答
　CD:DE=CH:HB=(6-42/39):42/39=(1-7/39):7/39=32：7

別解
２までは上と同じ
3　AEの長さ
　三平方の定理からAE=√(25/4)^2-5^2=15/4
４　答
　CD:DE=　三角形ABC:三角形ABE=AC×BC:AE×BE=５×６:15/4×7/4=32：7