第26回　 問題　（2月5日〜3月4日）

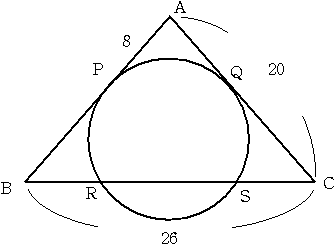
二等辺三角形ABCがあり、AB=AC=20cm　BC=26cmとなっています。
この二等辺三角形の二つの辺AB,ACと点P　点Qで接する円を描いたところ
AP=8cmとなりました。
このとき　この円がBCと交わる点をR,Sとします。
線分RSの長さはいくらでしょうか

解説
図のように補助線を引きます
赤い三角形と緑の三角形は相似になります。
　　　　　三角形BPRと三角形CRQにおいて
　　　　　　角PBR=角RCQ　（三角形ABCが二等辺三角形であるから）
　　　　　　角BPR=角PQR　（接弦定理）
　　　　　　　　　　=角CRQ　（ＰＱとＢＣが平行であり錯角の関係）
　　　　　よって三角形BPRと三角形CRQは相似になります

そこで対応する辺の比の関係　BR:CQ=BP:CRがわかります
BR=Xとします。CR=26−Ｘとなります　　これを代入すると
　Ｘ：12＝12:(26-X)　となり
　X^2-26X+144=0
　(X-8)(X-18)=0
　x=８，１８
　条件から　X<13X=8となります　
（X=18は　三角形BPSと三角形CSQの相似う使った時の答えになります。
同じ式が出てきます。）
　

よってRS=26-8×2=10　となります。　　　　

実は三角形RQPとも相似だったりする…

別の解き方

三角形ABHでピタゴラスの定理を使って　
　　　　　　AH=√(20^2-13^2)=√(33×７）=kとおく
三角形AOPと三角形ABHは相似であるから　
　　　　　　AO=20×8/k　OP=13×8/k=104/ｋ
　　　　　　OH=k-160/k=(k^2-160)/k=71/k
三角形ORHでピタゴラスの定理を使って　
　　　　HR^2=OR^2-OH^2=(104^2-71^2)/k^2
　　　　　　　　　　　　　　　　=175×33/(33×7)=25
よって　HR=5　RS=10