第25回　 問題　（12月19日〜２月4日）

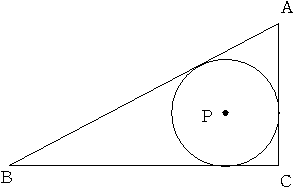
直角三角形ABCがあり、AB=5cm　BC=4cm　CA=3cmとなっています。
この三角形の内接円の中心をPとします。
直線ABと点Aで接し　点Pを通る円の半径を求めてください。

解答

直角三角形の内接円の半径をrとします。
　　Bから接点までの距離　4-r　Aから接点までの距離　3-rから　
　　(4-r)+(3-r)=5
　　r=1

　　　　三角形ABC=三角形ABP+三角形BCP+三角形CAPから
　　　　1/2×4×3=1/2×5×r+1/2×4×r+1/2×3×rとなり
　　　　r=1　としてもいいですね

上のように円の中心をO　OPとACの交点をＱとします。
ABが接線なので　APを弦とする接弦定理によって　角BAP=弦APに対する円周角=1/2×角AOP
一方Pが内心ですから　角BAP=1/2×角BAC
よって　角BAC=角AOP

また　角ABC=90°-角BAC　　　　　角OAP=90°-角BACから　三角形ABCと三角形OAPが相似であることがわかります。
角AＱO=90°ですから　Qは内接円とACの接点になっていることがわかり　AQ=3-1=2
BC:AQ=4:2=2:1　　OA=5×1/2=5/2となります。