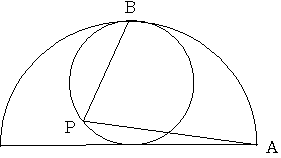
直径24cmの半円と その半円に内接する一番大きな円を考えます。
半円の弧 と内接円の接点をBとします。
Pをこの内接する円の円周上にとるとき
AP^2+BP^2の最小値をもとめてください。
記号:AP^2は APの長さを2乗することをあらわしています。
解答
第24回 問題 (12月5日〜2月4日)
直径24cmの半円と その半円に内接する一番大きな円を考えます。
半円の弧 と内接円の接点をBとします。
Pをこの内接する円の円周上にとるとき
AP^2+BP^2の最小値をもとめてください。
記号:AP^2は APの長さを2乗することをあらわしています。
解答
円の中心をOとして 円全体を描きます。
OP OBを結ぶと OBは小さい円の直径ですから角OPB=90°であることがわかります。
BPを延長して大きい円との交点をCとすると角OBP=90°から PはBCの中点であることがわかります。
三角形ABCに対して中線定理を使うと、 AP^2+BP^2=1/2(AB^2+AC^2)となります。
よって ACが最大のとき最大となり その値は AP^2+BP^2=1/2(AB^2+AC^2)= 1/2(24^2+12^2+12^2)=432 となります
解答2

実は当初考えていた解答は 次のようなものです
AP^2+BP^2=AD^2+PD^2+(OB^2-OP^2)
=AD^2+12^2-(OP^2-PD^2)
=AD^2+144-0D^2
=(AD+0D)(AD-OD)+144
=(AO+OD+OD)×OA+144
=(12+2×OD)×12+144
このことから ODが最大値のとき 最大に成ることがわかりODの最大は明らかに6でこのとき
AP^2+BP^2=(12+2×6)×12+144=432