第20回　 問題　（8月5日〜9月4日）　

解答1

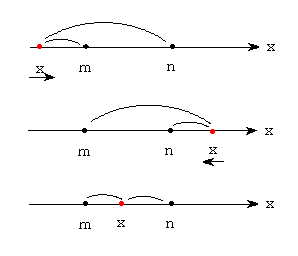
|x-m|+|x-n|について考えると　(ｘとmの距離)+（ｘとnの距離）を表すので上の図のように
x<=mでは単調減少　x>=nでは単調増加　　m<=x<=nでは一定となり
　m<=x<=nで最小値であることがわかります。

このことから　
|ｘ|+|x-10|　は　O<=x<=10で最小値　10
|x-1|+|x-9|は　1<=x<=9で最小値　8
|ｘ-2|+|x-8|は　2<=x<=8で最小値　6
|x-3|+|x-7|は　3<=x<=7で最小値　4
|ｘ-4|+|x-6|は　4<=x<=6で最小値　2
|x-5|はもちろん　x=5で最小値　0

以上から上の関数の和f(x)はx=5で最小値0+2+4+6+8+10=30となります。

解答2

たとえば2<=x<=3のとき上の絶対値は|x|　|x-1|　|x-2|　がそのまま外れ
のこりはマイナスがついて外れます。するとxの係数は3個が１、8個が-1となり
トータルf(x)=-5x+○のようになります。　つまりf(x)が単調減少となります。
xの係数がマイナスになるのは　絶対値の中から出てくる+xと-xの個数を考えればよいので
x<=5のときは必ず＋xは5個以下でf(x)のxの係数がマイナスである事がわかります。
逆にx>=5のときは＋xは6個以上でf(x)のxの係数はプラスとなります。
つまりこの関数は　x<=5で単調減少　x>=5で単調増加ですから
最小値はx=5のときで　5+4+3+2+1+0+1+2+3+4+5=30となります