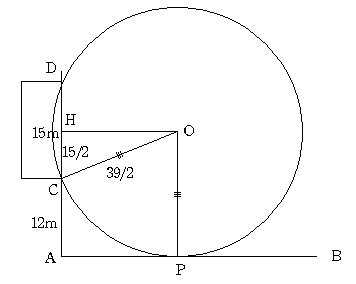ほげさんがゲームに参加しました。線分AB上のどの点からでも良いからフリーキックをして
ゴールに入ったら商品をもらえるというものです。AC=12m CD=15m 角BAD=90度 です。
さてほげさんはどの地点からキックをすると一番よいのでしょうか。APを求めてください。
ただしボールは途中でとまらないものとします。
キーパーはいません
ABは十分長いものとします
要するに 角CPDが最大であるときAPの長さを求めなさい ということです。
答え
まず円周角の公式を確認しておきましょう
同じ弦に対する円周角は等しい
つまり 円Oと弦ABがあるとして、円O上の任意の点Pに対して角APBはすべて同じ角になります。
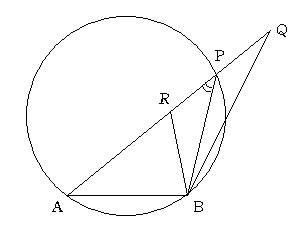
では 円の外の点をQとすると角度はどうなるか考えてみます。。ARと円との交点をPとすると
角APB=角AQB+角PBQですから 円の外に点があるときは角ARBの方が角APBより小さいことがわかります。
次に円の中の点Rについてはどうでしょう。ARを延長して円との交点をPとすると
角ARB=角APB+角PBRですから 円の中に点があるときは角ARBの方が角APBより大きいことがわかります。
次に下図のような補助円を書きます(円OはABに接し CDを弦としています)
すると上に書いたことから、図のP以外はすべてこの円の外にありますから AB上に点Qをとるとすべて角CPDより
小さいことがわかります。つまり図の点Pが求める点であることがわかります。