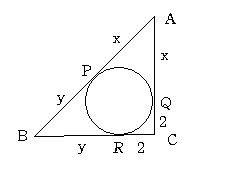
第15回　 問題　（3月5日〜4月4日）

各辺の長さが整数で、内接円の半径が2cmである直角三角形の斜辺の長さはいくらになりますか。

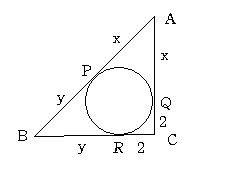
上の図のように記号をつけます　AB=c　BC=a　CA=ｂとします。
AB=x+y　AC+BC=(x+2)+(y+2)より　c=b+a+4
また　三角形の面積を考えると
1/2×(a+b+c)×2=1/2×a×bであるからここに代入して
a+b+b+a+4=1/2ab
ab-4a-4b=8
(a-4)(b-4)=8
a<=bとして一般性を失わないので　(a-4,b-4)=(1,8),(2,4)
(a,b)=(5,12),(6,8)　このときc=13,10

最後は有名な三角形になりました。勘を働かせてもできそうだけど　
上のような計算でうまく答えが出たときは自分自身で嬉しかったので問題にしました。(^.^)