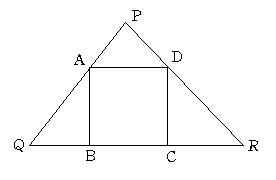
正方形ABCDと三角形PQRがあります。上のように、点Q,B,C,Rが同一直線上に、
点P,A,Qが同一直線上に、点P,D,Rが同一直線上にあります。
正方形ABCDの面積をS、三角形PQRの面積をTとするとき、T/Sの最小値を求めてください。
teki さんの算数的解答
一般的には、三角形に内接する長方形(正方形ではありません。)は、三角形の
面積の1/2を超えません。証明します。
三角形の内部に長方形を内接させた場合、長方形の高さが三角形の高さの丁度半分
の時、長方形の外側の部分をおり返せば、ぴったり長方形と重なります。
高さがこれより大きくても小さくても、長方形の外側にはみ出したり、おり返した部分が
重なります。
従って、長方形の面積は、三角形の面積の1/2以上にはなり得ません。
問題のケースは、正方形ですが、正方形も長方形の一種ですので、その面積は三角形
の面積の1/2以上にはなり得ないのです。
すなわちT/Sは、A,DがそれぞれPQ,PRの中点の時最大で、2となります。
わたしの解答
正方形ABCDの一辺の長さを1とします。S=1ですね。
三角形PADの(ADを底辺としたときの)高さをaとします。
三角形PADと三角形PQRは相似ですから、a:1=(a+1):QRより QR=(a+1)/a
三角形PQRの面積Tは 1/2×(a+1)/a×(a+1)=(a+1)^2/2a=1/2×(a+2+1/a) …①
ここでa>0から相加平均と相乗平均の公式からa+1/a≧2√(a×1/a)=2
よって①から T≧1/2×(2+2)=2 すなわち S/Tの最小値は2となります。