第6回　 問題　（5月5日〜6月4日）

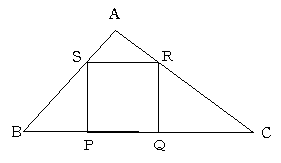
三角形ABCについて、AB=15cm　BC=14cm　CA=13cm　であるとします（図はとっても不正確です）
この三角形の中に正方形PQRSを図のように、ＰＱはBC上に,RはCA上に,SはAB上にあるように描きます。
正方形PQRSの一辺の長さはいくらでしょうか。

　以下は問題ではありませんが、出来た人は、コンパスと定規のみで正方形を描く方法を考えてみてください

解
まず三角形ABCの高さをもとめます。
　AからＢＣに垂線を下ろしてその足をＨとすると直角三角形ABHは15:12:9(5:4:3)で,直角三角形ACHは13:12:5になっている
というのは有名な事らしいです。他のHPで勉強しました。いつか使ってやろうと思っていた事です。
　高校生以上になるとヘロンの公式から面積を出し、高さ12cmを出すでしょう。
　中学程度の知識では三平方の定理から　AH^2=AB^2-BH^2=AC^2-CH^2　BH=xとおいて　15^2-x^2=13＾2-(14-x)^2
15^2-13^2=x^2-(14-x)^2A^2-B^2=(A+B)(A-B)の公式から　28×2=14(2x-14)　x-7=2　x=9となります。
これからAH=12cmとなります。

次にSPを求めます
正方形の一般の長さを12aと置きます。三角形ABHと三角形SBPが相似なのでBP=9a
三角形AHCと三角形ＲＱＣが相似なのでCQ=5a
BC=BP+PQ+QC=9a+12a+5a=26a=14より　12a=14×12/26=84/13となります。

また、次のようにしても求まります。面積を考えて台形と上の三角形の和から
1/2x(14+x)+1/2x(12-x)=1/2×14×12　を解きます。
　

追加問題の答え
さて、この図形をコンパスと定規だけで描く方法は次のとおりです。
まずAB上に任意の点Ｓ’をとり、Ｓ'からBCに垂線を下ろしP'とします。
まずS'P'を一辺とする正方形S'P'Q'R'を描きます。
次にBをR'を結ぶ直線とACとの交点を求めるとそれがRになります。
あとはＲからBCへ垂線を下ろしRを中心に半径RQの弧とABの交点がＳという風にS,Pを求めます。

なぜこれで描けるか考えてみてください。

コメント
この問題は、コンパスのみで何かをするというtomhさんの問題から考えたものです。
ということはそれまで今月の問題は考えられなかったという事になります(~o~)
先行き不安でしょう。(~_~)　安心してください。仲間がいます。私も不安です。

この問題は算数問題にしたかったのですが、どうしても高さを算数で出せないのと
問題をかえると相似がばればれになるので、どうにかしたかったのですが、
うまくまとめれなかった問題です。