第4回　 問題　（3月5日〜4月4日）
x/sinx=6πの解の数はいくつありますか（角はラジアンです）

解１noetherさん 老眼鏡さん　tekiさん
与えられた方程式はx<>0 かつ sinx=x/(6π)・・・★
と同値。
ここでx/(6π)>1 ⇔ x>6π だから、★はx>6πでは解を持たない。
またsinx のグラフを考えると、★は
区間(0,π)で1個,区間(2π,3π)と(4π,5π)でそれぞれ2個の解をもつ。
よって★はx>0の範囲で5個の解をもつ。
x<0の範囲でも全く同様なので、ゆえに求める個数は「10個」

解２　巷の夢さん　小杉原　啓さん　モルモット大臣さん　清川育男さん
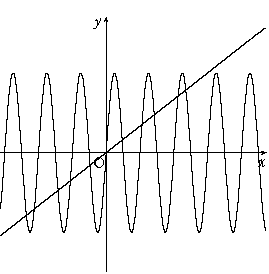
ｙ＝ｘとｙ＝６πsinｘの交点から求めました。
ｘ＝０の時は左辺が１に収束し、６πでないので
除外します。

解3　有無相生さん

f(x)=x/sin (x)のグラフを書いて、ｙ＝6πとの交点を求めました。

解4　Qperさん
グラフを描きました。
y=1/x,y=sinxを描いて積をとりました。
0<x<?で1個、2?<x<3?で2個、4?<x<5?で2個、後はグラフの対称性より2倍して