戞104夞丂嶼悢栤戣丂乮11寧5擔乣12寧4擔乯
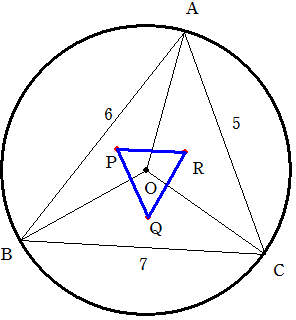
AB=6 BC=7 CA=5丂偺嶰妏宍ABC偑偁傝偦偺奜愙墌偺拞怱傪O偲偟傑偡丅
嶰妏宍OAB偺廳怱傪P丂嶰妏宍OBC偺廳怱傪Q丂嶰妏宍OCA偺廳怱傪R偲偟傑偡丅
嶰妏宍PQR偺柺愊偲丂嶰妏宍ABC偺柺愊偺斾偼偄偔傜偵側傞偱偟傚偆偐丅

夝摎
P偼廳怱偱偁傞偐傜丂OP偲AB偺岎揰傪D偲偡傞偲D偼AB偺拞揰...丂嘆
R偼廳怱偱偁傞偐傜丂OR偲AC偺岎揰傪E偲偡傞偲E偼AC偺拞揰...嘇
OP:OD=2:3丂OR:OE=2:3偲側偭偰偍傝丂嶰妏宍OPR偲嶰妏宍ODE偼憡帡偱偁傝丂
憡帡斾偼2:3丂偐偮丂PR偲DE偼暯峴偱偁傞丅
拞揰楢寢掕棟偐傜丂DE偼BC偲暯峴偱DE=1/2BC
傛偭偰丂PR傕BC偲暯峴偱PR=2/3DE=1/3BC
摨條偵PQ偼AC偲暯峴偱丂PQ=1/3AC
傛偭偰丂嶰妏宍QRP丂偲丂嶰妏宍ABC偼憡帡偱憡帡斾偑俁丗侾
柺愊斾偼丂俁丗侾丂丂丂丂丂丂丂丂丂丂丂丂