第95回　算数問題　（1月5日〜2月4日）

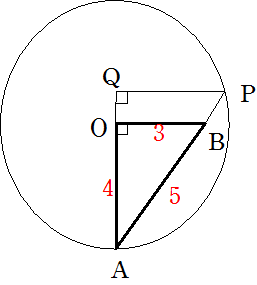
図のようにOA=4cm　AB=5cm　BO=3cmの直角三角形があります。
Oを中心　OAを半径として円を描き　ABの延長と円との交点をPとします。
OBと平行でPを通る直線とAOの延長との交点をQとします。
OQの長さはいくらでしょうか。

解答１
　点Oから弦APに垂線を下ろし足をHとします。
三角形OAB∽三角形HAOですから　OA:AH=５：４
よって　AH=４×４／５＝１６／５　となります。
AP=２×AH=32/5
三角形OAB∽三角形QAPより　AP:AQ=5:4
よってAQ=３２／５×４／5=128／25
OQ=128/25-4=28/25　となります。
解答２　数学の範囲の解答です　
直線OBと円の交点のうちBに近い方をC　Bから遠いほうをDとします。
方べきの低利からAB×BP=　BC×BDより　BP=７×１/５=7／5
OBとQPが平衡であるから　AO:OQ=AB:BP
よって　OQ=４×7／5×1/５=28/25

解答３
　ACが直径となるように点Cを円周上にとります。
Oから弦APに垂線を下ろし足をHとします。
三角形OAB∽三角形PACですから　AC:AP=５：４
よって　AP=８×４／５＝32/5
三角形OAB∽三角形QAPですから　AQ:AP=４：５
よって　AQ=32/5×4/5=128/25
よって　OQ=128/25-4=28/5