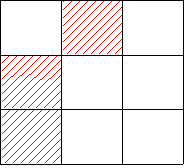
図のように9つの正方形のうち3箇所のみを赤で塗るものとします。回転して重なる塗り方は1通りとして考えると
全部で何通りの塗り方があるでしょうか。。
解答
3つ適当に塗ったときに全部で 9C3=84通りの塗り方があります。
この84通りの塗り方をしたときに 回転して重なるものが4つあるグループと 2つあるグループがあります。
回転して重なるものが2つあるグループは 真ん中縦に3つ塗ったときと真ん中横に3つぬったもの
右上から左下に対角線状に3つ塗ったものと左上から右下に対角線状に3つ塗ったもの
よって (84-4)/4=20が 4つあるグループの数
以上から 20+2=22通りとなります。
解答 2
まん中を塗るとき 少なくとも1つは角に塗るとき 右上に塗ったとして 残りは角のとき 隣か向かいか 2通り
残りが辺のとき4通り
残り2つとも辺の時隣か向かいか2通り
真ん中を塗らないとき 3つとも角のとき 1通り
2つが角のとき 先に辺を1つ塗って残り4つのうちの2つの角を塗る4×3/2=6通り
1つが角のとき 上の6通りのものを時計方向に1つ面して塗るから6通り
3つとも辺のとき 1通り
以上から 2+4+2+1+6+6+1=22通り