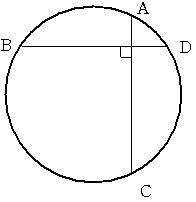
図のように周囲の長さが60cmの円があります。弧ABは弧ADより8cm長く 弧BCは弧ABより12cm長くなっています。
このとき弧CDの長さを求めてください。
解答 17cm
第93回 算数問題 (11月5日〜12月4日)

図のように周囲の長さが60cmの円があります。弧ABは弧ADより8cm長く 弧BCは弧ABより12cm長くなっています。
このとき弧CDの長さを求めてください。
解答 17cm
解1
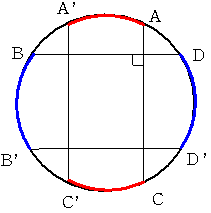
図のように 弦ACに対し左右対称に弦A'C' 弦BDに対し上下対称に弦B'D'を描きます。
条件から 弧AA'=弧CC'=8 弧BB'=DD'=12となります。
弧AD=弧A'B=弧B'C'=弧CD' ですから 60-2×(8+12)=20
弧CD'=20÷4=5
弧CD=5+12=17であることがわかります。
解2
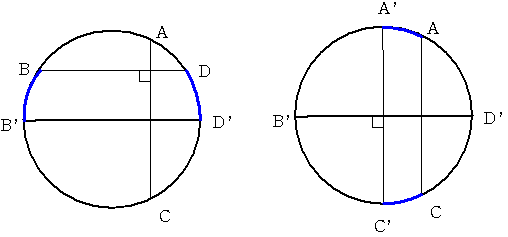
BDに平行に直径B'D'を描きます すると
AD+BC=(AD'-DD')+(BB'+B'C)=AD'+B'C となります。
ACと平行に直径A’C'を描きます すると
AD'+B'C=(A'D'-AA')+(B'C'+CC')=A'D'+B'C' となります。
よって 向かいあう2つの弧の長さの和は円周の半分であることがわかります。
このことから BCは ADよりも8+12=20cm長く BCとADの長さの和は 60÷2=30であるから
ADの長さは (30-20)÷2=5であることがわかります。
よって ABは 5+8=13cm
ABと CDの長さの和も30cmですから CD=30-13=17cmであることになります。