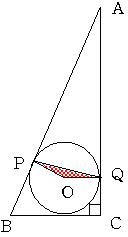
上の図のようにAB=13cm BC=5cm CA=12cmの直角三角形と Oを中心とするこの直角三角形の内接円がある。
円とAB,ACとの接点をP,Qとするとき 三角形OPQの面積はいくらになるでしょうか
解答
前半 円の半径を求める
解1
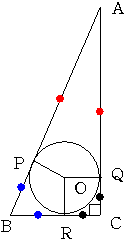
円OとBCの接点をRとする
図の○の長さは同じであるから 赤○+青○=13
AC+BC=赤○+青○+黒○+黒○=5+12=17
13+黒○+黒○=17
よって 黒○=2
これより 内接円の半径は2cmであることがわかる。
解2
三角形の面積を考えると 内接円の半径をrとして
三角形ABO+三角形BCO+三角形CAO=三角形ABCから
1/2×(13r+5r+12r)=1/2×5×12より
30r=5×12
r=2
後半 面積を求める
解1
OQの延長線上に点Pからおろした垂線をHとする
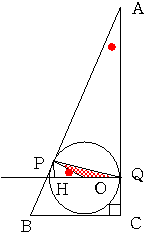
三角形ABCと三角形OPHは相似であるから
PH=2×5/13=10/13
よって三角形OPQ=1/2×2×10/13=10/13
解2
三角形ABC=1/2×5×12=30
AP=AQ=12-2=10より
三角形APQ=30×10/13×10/12=250/13
三角形OBC=1/2×5×2=5
5角形OPBCQ=2×三角形OBC=2×5=10
よって 三角形OPQ=三角形ABC-三角形APQ-5角形OPBCQ
=30-250/13-10
=20-250/13=10/13