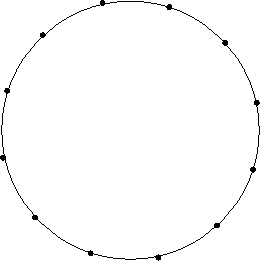
上の図のように円周上に等間隔に12個の点を取ります。この点から3点を選んで結び 三角形を描くとき
互いに合同でないものは全部でいくつあるでしょうか。
解答 12通り
ある辺を結んだときの間の弧の長さがn/12のときにn とあらわすことにします。
12を3つの正の数の和にする方法は 11C2=55
Ⅰ 3辺とも同じ長さのとき
(4,4,4)の1通り
Ⅱ 2辺の長さが同じとき
2x+y=12 0<x<12 0<y<12 x≠y
から 0<12-2x<12 よって 0<x<6 x≠4 4通り (1,1,10) (2,2,8) (3,3,6) (5,5,2)
Ⅲ 3辺の長さが異なるとき
(55-1-3×4)/6=7
よって 7+4+1=12通り