第83回　算数問題　（1月５日〜2月4日）

図のように　三角形ABCの　辺AB　辺BC　辺CA上に　点K　点L　点M　を
AK:KB=BL:LC=CM:MA=３：１となるようにとります。
ALとCKの交点をP　BMとALの交点をQ　CKとBMの交点をRとします。
このとき　三角形PQRと三角形ABCの面積比を簡単な整数比で求めてください。

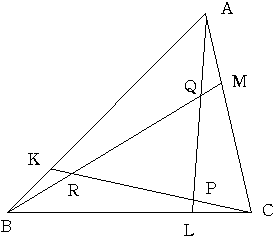
Mを通りALに平行な直線と辺BCの交点をSとします。
ALとMSが平行でAM:MC=１：３よりLS:SC=1:3
BL:LC=３：１より　BL:LS:SC=12：1：3
QLとMSが平行で　BL:LS=12：1より　BQ:QM=12：1

三角形ABQ=12/13×三角形ABM=12/13×1/4×三角形ABC=3/13×三角形ABC
三角形BCR　三角形CAPも同様であるから
三角形PQR=三角形ABC-三角形ABQ-三角形BC-　三角形CAP
　　　　　　　 =(1-3/13×3)×三角形ABC
　　　　　　　 =4/13×三角形ABC
よって面積比は4：13