第81回　算数問題　（11月12日〜12月4日）

三角錐OABCがあり、OA=OB=OC=８　BC=CA=AB=４となっています。
辺OB,OC上にそれぞれ点P,Qを取り、　L=AP+PQ+QAとします。
Lの最小値はいくらになるでしょうか


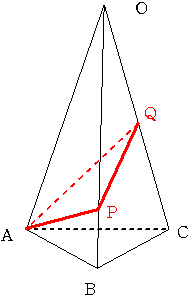
上図のように底面のない展開図を描くと　A,P,Q,A'が一直線になっているときが最小であることがわかる。
三角形OAPと三角形OA'Qは合同であるから　OP=OQ
　　　合同の理由　三角形OABと三角形OA'Cが合同であるから　OA=OA'
　　　　　　　　　　　　OA=OA'から　三角形OAA'は二等辺三角形となり　角OAB=角OA'Q
　　　　　　　　　　　　三角形OABと三角形OA'Cが合同であるから　角AOB=角A'OQ
よって三角形OPQは二等辺三角形であり　三角形OPQと三角形OBCは相似であるから
BCとPQは平行となる

角APB=角OPQ=角OBC=角ABPであるから　三角形ABPは三角形OABと相似な二等辺三角形となっており
OA:AB=AB:BPより　８:４=４:BP　となり　BP=２

三角形OPQと三角形OBCについて　OP:OB=PQ：BCより　6:PQ=８：４　となり　PQ=3

以上より　AA'=AP+PQ+QA'=AB+3+A'C=4+3+4=１１