第80回　算数問題　（10月5日〜11月4日）

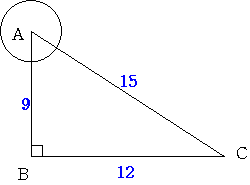
図のようにAB=9cm　BC=12cm　CA=15cmの直角三角形があります。
半径１cmの円が、この直角三角形の頂点または辺を中心とするように動く時
直角三角形の内部で　この円が通過した部分の面積はいくらになるでしょうか。

解答１

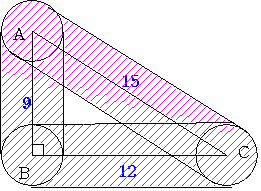
円が通過する部分は図のようになる。
内部にある通過していない三角形に着目する。

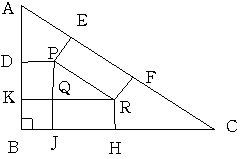
内分の三角形から　各辺に垂線を下ろし　図のように記号をつける。
PQ=３ｘ　とおくと　QR=4ｘ　PR=５ｘ
AE=AD=9-3ｘ-1=8-3ｘ
CF=CH=12-4x-1=11-4ｘ
AC=AE+EF+CF=(8-3ｘ）+5ｘ+(11-4ｘ)=15より　2ｘ＝4　x=2
PQ=6　であるから　三角形ABCと三角形PQRの辺の長さの比は　9:6=3：2
面積比は　9：4
よって　通過した部分の面積は　三角形ABC×5/9=1/2×9×12×5/9=30

解２
三角形ABCの内心と　三角形PQRの内心は一致する
三角形ABCの内心の半径をｒとすると
1/2×9×12=1/2×(9+12+15)×ｒ　　より　r=3
よって　三角形PQRの内心の半径は　3-1=2
三角形ABCと三角形PQRの辺の長さの比は　3：2　　面積比は　9：4
よって　通過した部分の面積は　三角形ABC×5/9=1/2×9×12×5/9=30