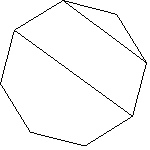
第79回　算数問題　（9月5日〜10月4日）

正８角形の頂点同士を線分で結び正８角形を分割します。
2本の線分を引いたときに３つに分割する方法は何通りありますか。
ただし、各頂点は区別するものとし、２つの線分はその端点を共有しないものとします。

解答１
３つに分割された真ん中の図形について場合分けをする
　（３分割された図形のうち２つの線分で囲まれた図形）
場合１　６角形
１−１　辺１→線分→辺３→線分となっているとき
　辺１を固定すると図形は１通りのみ　よって　8通り

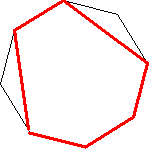
１−２　辺２→線分→辺２→線分
　辺２を固定すると図形は１通りのみ　よって４通り

場合２　５角形
辺１→線分→辺２→線分
　辺１を固定すると図形は２通り　　よって２×８＝１６通り

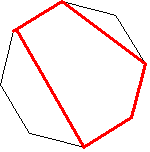
場合３　４角形
辺１→線分→辺１→線分
辺１を固定すると３通り　重複を考えて　3×８÷２=12通り

以上より　8+4+16+12=４０通り


解答２
１本の線分の引き方
　各頂点から隣り合わない頂点に線を引く方法は　５通り
　頂点は８つで　重複がそれぞれ３つあるから　８×５÷２=２０　通りある

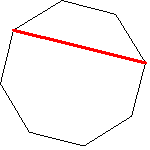
２本の線分の引き方
　20本の線分のなかから２本選ぶので　20C2=１９０通り

２本の線分が交差する場合
　８つの頂点から　４つの頂点を選ぶ方法は　8C4=70通り
４つの頂点を結ぶ四角形の２つの対角線を描くと　これは正８角形に２本の線分を交差するように描いていおり
重複せずにすべての場合を尽くしている。
よって７０通り

２本の線分が１つの頂点を共有する場合
１つの頂点から　５本の線分が描けるので　頂点ごとに　5C2=10通り　全手の頂点について　10×８=80通り

以上から
190-70-80=４０通り