第76回　算数問題　（6月5日〜76月4日）

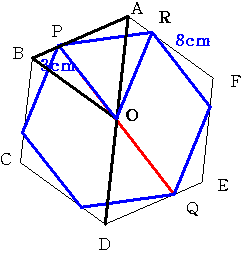
図のように一辺が8cmの正6角形の辺AB,辺DE上に　BP=QE=3cmとなる点P,Qをとります。
PQの長さはいくらになるでしょうか。

解答

正６角形ABCDEFの中心をOとします。
上図のようにP、Qを互いに向かいあった頂点とし　Oを中心とする正６角形を描きます。
三角形OABの面積を　8×8＝64　とすると
三角形APRの面積は　3×5=15
青い正６角形の面積は　6×(64-15）=6×49
正三角形OPRの面積は　49　となる。
ABの長さが8cmであるから　PRの長さは　７cmとなり　PQ=２×PR=14cmとなる。



解２　中学数学の範囲では　三平方を使うと簡単にでますね

三平方の定理から　PQ^2=(8√3)^2+2^2=256　
PQ=１４

解３　高校数学の範囲では
三角形OBPに余弦定理を使う　解答省略